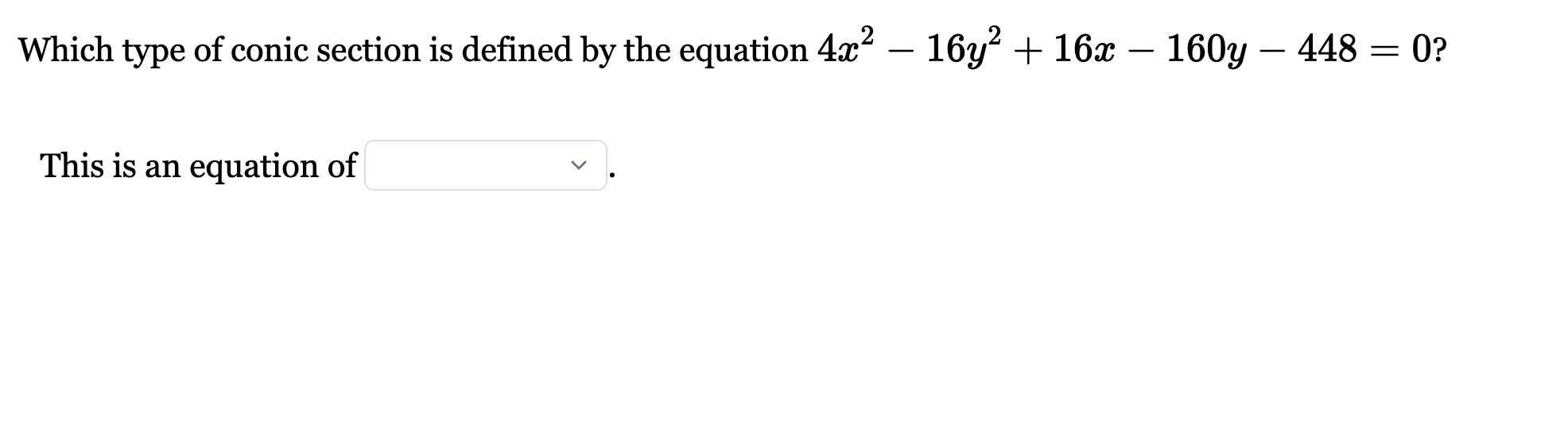Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which type of conic section is defined by the equation 4x^(2)-16y^(2)+16 x-160 y-448=0 ? This is an equation of

Which type of conic section is defined by the equation 4x2−16y2+16x−160y−448=0 4 x^{2}-16 y^{2}+16 x-160 y-448=0 ?\newlineThis is an equation of

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Find the vertex of the transformed functionright chevron icon

Full solution

Q. Which type of conic section is defined by the equation 4x2−16y2+16x−160y−448=0 4 x^{2}-16 y^{2}+16 x-160 y-448=0 ?\newlineThis is an equation of
  1. Simplify Equation: Step 11: Simplify the equation by grouping similar terms. 4x2+16x−16y2−160y−448=04x^2 + 16x - 16y^2 - 160y - 448 = 0
  2. Rearrange for Identification: Step 22: Rearrange the equation to make it easier to identify. 4x2+16x−16y2−160y=4484x^2 + 16x - 16y^2 - 160y = 448
  3. Divide and Simplify: Step 33: Divide the entire equation by 44 to simplify.x2+4x−4y2−40y=112x^2 + 4x - 4y^2 - 40y = 112
  4. Complete the Square: Step 44: Complete the square for the xx-terms and yy-terms.(x2+4x)−4(y2+10y)=112(x^2 + 4x) - 4(y^2 + 10y) = 112Adding and subtracting 44 inside the first parenthesis and 100100 inside the second parenthesis:(x2+4x+4−4)−4(y2+10y+25−25)=112(x^2 + 4x + 4 - 4) - 4(y^2 + 10y + 25 - 25) = 112(x+2)2−4−4((y+5)2−25)=112(x + 2)^2 - 4 - 4((y + 5)^2 - 25) = 112(x+2)2−4(y+5)2+100=112(x + 2)^2 - 4(y + 5)^2 + 100 = 112
  5. Further Simplification: Step 55: Simplify the equation further.\newline(x+2)2−4(y+5)2=12(x + 2)^2 - 4(y + 5)^2 = 12
  6. Identify Conic Section: Step 66: Identify the type of conic section.\newlineThe equation (x+2)2−4(y+5)2=12(x + 2)^2 - 4(y + 5)^2 = 12 is in the form of a hyperbola because it has one squared term subtracted from another squared term.

More problems from Find the vertex of the transformed function

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 1 month ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 1 month ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 1 month ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 1 month ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 1 month ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 2 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 2 months ago

View all (169)