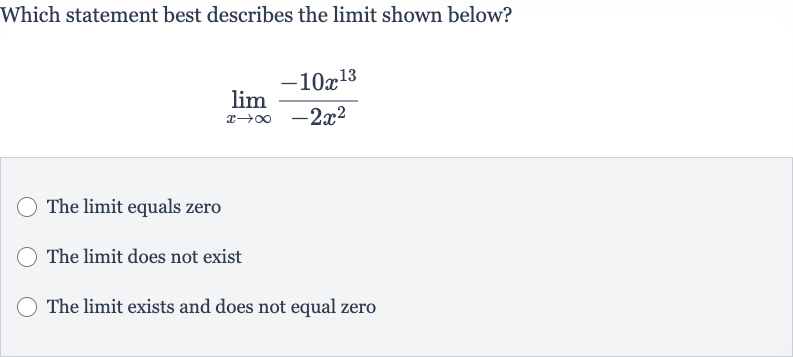Full solution
Q. Which statement best describes the limit shown below?The limit equals zeroThe limit does not existThe limit exists and does not equal zero
- Simplify expression: We are given the limit expression:First, we simplify the expression by dividing both the numerator and the denominator by , the highest power of in the denominator.
- Further simplification: The simplified expression becomes: This simplifies to:
- Divide coefficients: Now we can further simplify the expression by dividing the coefficients: This simplifies to:
- Approaching infinity: As approaches infinity, the term will also approach infinity since any positive power of will grow without bound as becomes larger and larger.Therefore, the limit of as approaches infinity is infinity.
- Final statement: Since the limit of the function as approaches is , the correct statement is:"The limit exists and does not equal ."
More problems from Power rule
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help