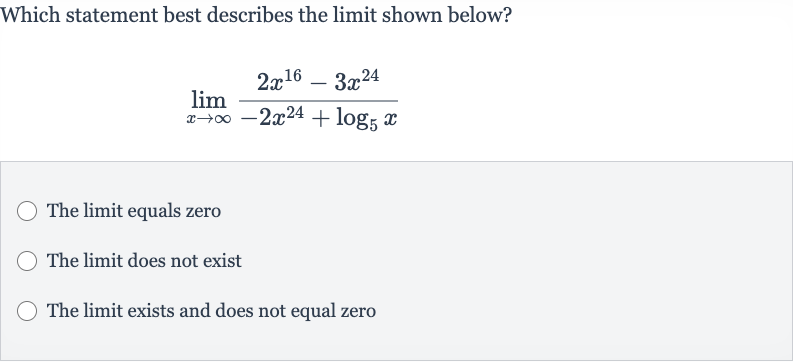Full solution
Q. Which statement best describes the limit shown below?The limit equals zeroThe limit does not existThe limit exists and does not equal zero
- Analyze Behavior as Approaches Infinity: We need to analyze the behavior of the function as approaches infinity. To do this, we will compare the degrees of the polynomials in the numerator and the denominator.
- Compare Highest Degree Terms: The highest degree term in the numerator is and in the denominator is . As approaches infinity, the terms with lower degrees become insignificant compared to the highest degree terms.
- Simplify by Dividing Highest Power: We can simplify the limit by dividing both the numerator and the denominator by , the highest power of present in the expression.
- Simplify as Approaches Infinity: As approaches infinity, and both approach . Therefore, the limit simplifies to:
- Conclusion: The limit exists and does not equal zero. The correct statement is "The limit exists and does not equal ."
More problems from Power rule
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help