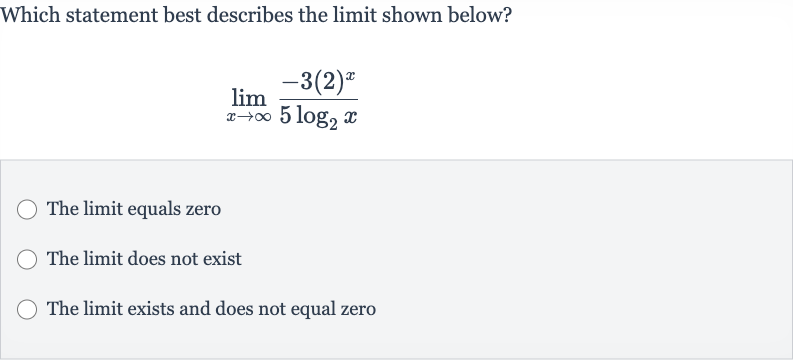Full solution
Q. Which statement best describes the limit shown below?The limit equals zeroThe limit does not existThe limit exists and does not equal zero
- Given Limit Expression: We are given the limit expression . To analyze the behavior of this limit, we need to consider the growth rates of the numerator and the denominator as approaches infinity.
- Analysis of Growth Rates: The numerator grows exponentially as approaches infinity. Exponential functions grow much faster than polynomial or logarithmic functions.
- Numerator Behavior: The denominator is a logarithmic function, which grows much slower than the exponential function in the numerator. As approaches infinity, the logarithmic function increases without bound, but at a much slower rate than the exponential function.
- Denominator Behavior: Since the numerator grows much faster than the denominator, the fraction as a whole will grow without bound. However, because the numerator is negative, the fraction will tend toward negative infinity.
- Limit Conclusion: Therefore, the limit does not exist because the expression diverges to negative infinity. The correct statement is "The limit does not exist."
More problems from Power rule
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help