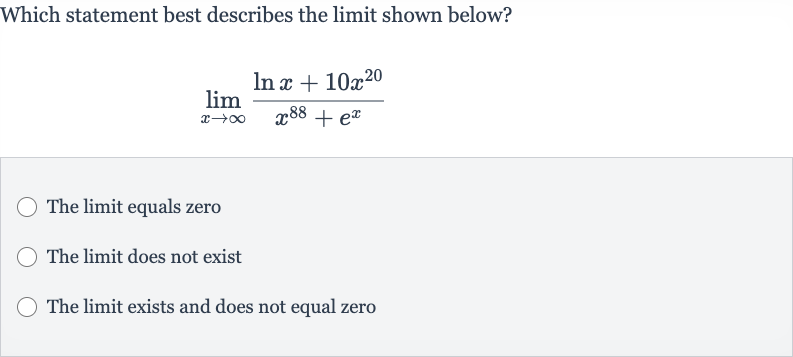Full solution
Q. Which statement best describes the limit shown below?The limit equals zeroThe limit does not existThe limit exists and does not equal zero
- Analyze Behavior: We need to analyze the behavior of the numerator and the denominator as approaches to determine the limit.
- Numerator Growth: The numerator grows without bound as approaches infinity, but at a much slower rate than because the logarithmic function grows slower than any polynomial.
- Denominator Growth: The denominator also grows without bound as approaches infinity. However, grows much faster than any polynomial, including .
- Comparison of Growth Rates: Since in the denominator grows faster than any term in the numerator, the fraction as a whole approaches zero as approaches infinity.
- Limit Conclusion: Therefore, the limit of as approaches infinity is .
More problems from Power rule
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help