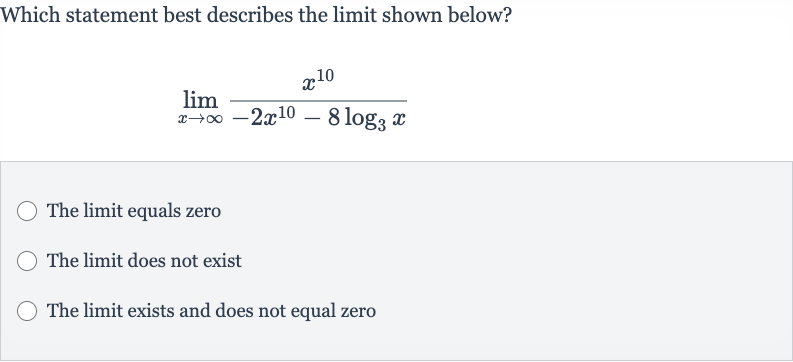Which statement best describes the limit shown below? lim_(x rarr oo)(x^(10))/(-2x^(10)-8log_(3)x) The limit equals zero The limit does not exist The limit exists and does not equal zero

Question

Which statement best describes the limit shown below?  lim_(x rarr oo)(x^(10))/(-2x^(10)-8log_(3)x) The limit equals zero The limit does not exist The limit exists and does not equal zero

Bytelearn · Accepted Answer

Given Limit Expression: We are given the limit expression: lim_(x rarr oo)(x^(10))/(-2x^(10)-8log_(3)x) To find the limit as x approaches infinity, we need to analyze the behavior of the numerator and the denominator separately.Highest Power Analysis: First, let's focus on the highest power of x in both the numerator and the denominator. In the numerator, the highest power is x^(10). In the denominator, the highest power is also x^(10), which is in the term -2x^(10).Simplify by Dividing: Since the highest power of x in both the numerator and the denominator is the same, we can simplify the expression by dividing both the numerator and the denominator by x^(10). lim_(x rarr oo)(x^(10)/x^(10))/(-2x^(10)/x^(10)-8log_(3)x/x^(10))Limit as x Approaches Infinity: Simplifying the expression, we get: lim_(x rarr oo)(1)/(-2-8log_(3)x/x^(10)) As x approaches infinity, the term 8log_(3)x/x^(10) approaches zero because the logarithmic function grows much slower than the polynomial function.Simplify Limit: Now, the limit simplifies to: lim_(x rarr oo)(1)/(-2-0) Which is simply: lim_(x rarr oo)(1)/(-2)Final Result: The limit of a constant over a constant is just the division of those constants. Therefore, the limit is: 1/(-2) = -1/2Conclusion: Since we have found a finite value for the limit, the correct statement is that the limit exists and does not equal zero.

Which statement best describes the limit shown below? $\newline$ $\lim _{x \rightarrow \infty} \frac{x^{10}}{-2 x^{10}-8 \log _{3} x}$ $\newline$ The limit equals zero $\newline$ The limit does not exist $\newline$ The limit exists and does not equal zero

Full solution

More problems from Power rule

Related topics