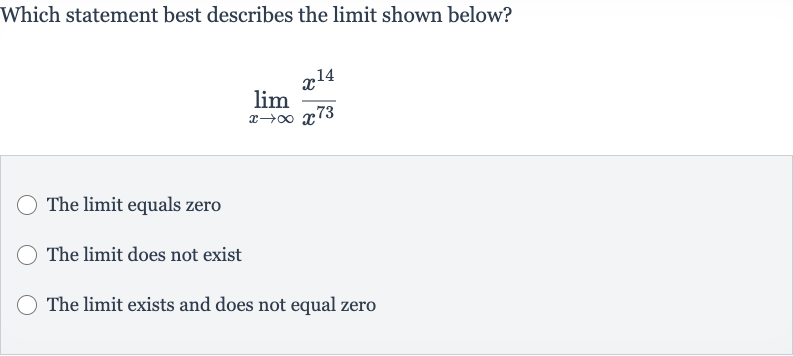Full solution
Q. Which statement best describes the limit shown below?The limit equals zeroThe limit does not existThe limit exists and does not equal zero
- Given Limit Expression: We are given the limit expression . To find the limit as approaches infinity, we need to analyze the behavior of the function.
- Simplify by Subtracting Exponents: We can simplify the expression by subtracting the exponents of in the numerator and the denominator since they have the same base and we are dividing them.
- Analysis of Function Behavior: After subtracting the exponents, we get:This means that as approaches infinity, the function is raised to the power of negative fifty-nine.
- Negative Exponent Interpretation: A negative exponent means that the function is the reciprocal of raised to the positive exponent. Therefore, is equivalent to .
- Approaching Zero: As approaches infinity, the denominator becomes larger and larger, making the whole fraction smaller and smaller, approaching zero.
More problems from Power rule
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help