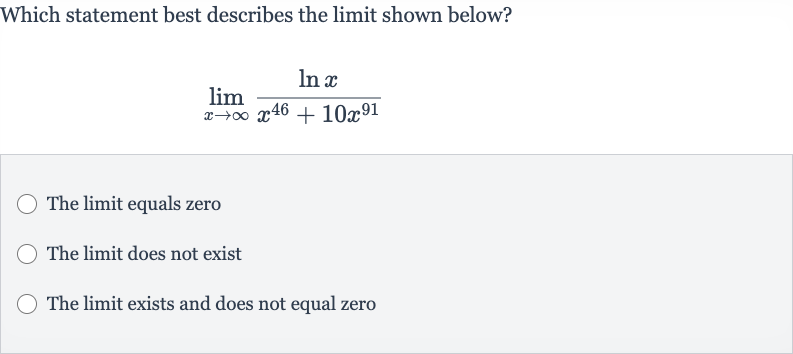Full solution
Q. Which statement best describes the limit shown below?The limit equals zeroThe limit does not existThe limit exists and does not equal zero
- Given Limit Expression: We are given the limit expression . To determine the behavior of this limit, we need to analyze the growth rates of the numerator and the denominator as approaches infinity.
- Analysis of Growth Rates: The numerator grows logarithmically, which is much slower than any positive power of . The denominator has two terms: and . As approaches infinity, the term with the highest power of will dominate the growth of the denominator. In this case, it's the term.
- Comparison of Numerator and Denominator: Since the denominator grows much faster than the numerator, the fraction as a whole will approach as approaches infinity. This is because the denominator's growth will make the fraction's value smaller and smaller.
- Conclusion: Therefore, the correct statement that describes the limit is: "The limit equals ."
More problems from Power rule
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help