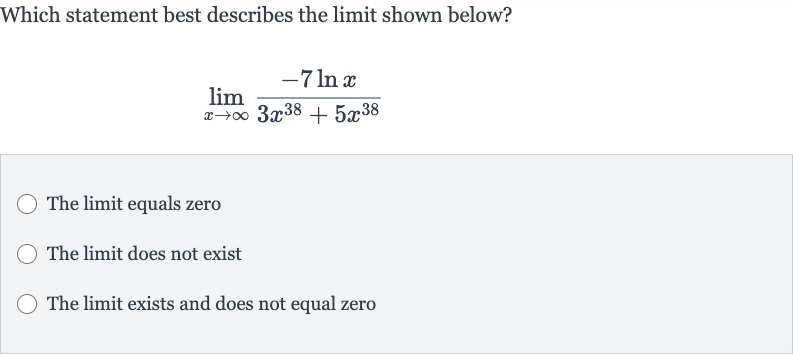Full solution
Q. Which statement best describes the limit shown below?The limit equals zeroThe limit does not existThe limit exists and does not equal zero
- Identify Denominator: We are given the limit expression . To find the limit as approaches infinity, we need to analyze the behavior of the numerator and the denominator separately.
- Combine Like Terms: First, let's look at the denominator: . We can combine like terms by adding the coefficients of the terms.
- Analyze Behavior: Now, we have the limit expression simplified to . The next step is to recognize that as approaches infinity, the natural logarithm function grows without bound, but at a much slower rate than any positive power of .
- Recognize Growth Rates: Since the denominator contains raised to the power, it will grow much faster than the natural logarithm in the numerator as approaches infinity. This means that the fraction as a whole will approach zero.
- Determine Limit: Therefore, the limit of as approaches infinity is because the denominator increases much faster than the numerator.
More problems from Power rule
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help