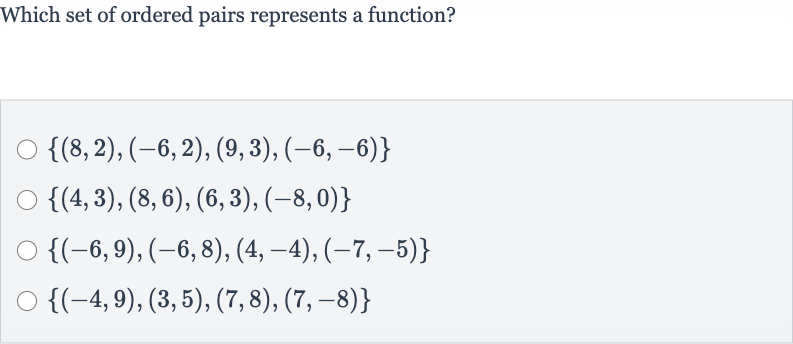AI tutor
Full solution
Q. Which set of ordered pairs represents a function?
- Definition of a Function: A function is defined as a set of ordered pairs where each input ( extit{x}-value) is associated with exactly one output ( extit{y}-value). To determine which set of ordered pairs represents a function, we need to check if any extit{x}-value is repeated with different extit{y}-values.
- Checking First Set: Let's examine the first set: Here, the -value is associated with two different -values: and . This violates the definition of a function.
- Checking Second Set: Now, let's examine the second set: In this set, each -value is unique and is associated with only one -value. This set represents a function.
- Checking Third Set: We do not need to check the remaining sets because we have already found a set that represents a function. However, for completeness, let's quickly check them.
- Checking Fourth Set: The third set is: Here, the -value is associated with two different -values: and . This set does not represent a function.
- Checking Fourth Set: The third set is: Here, the -value is associated with two different -values: and . This set does not represent a function.The fourth set is: Here, the -value is associated with two different -values: and . This set does not represent a function.
More problems from Write a quadratic function from its x-intercepts and another point
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help