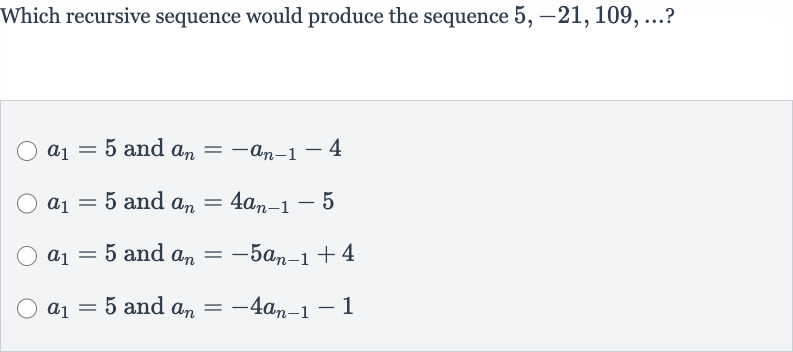Which recursive sequence would produce the sequence 5,-21,109,dots ? a_(1)=5 and a_(n)=-a_(n-1)-4 a_(1)=5 and a_(n)=4a_(n-1)-5 a_(1)=5 and a_(n)=-5a_(n-1)+4 a_(1)=5 and a_(n)=-4a_(n-1)-1

Question

Which recursive sequence would produce the sequence  5,-21,109,dots ?  a_(1)=5 and  a_(n)=-a_(n-1)-4  a_(1)=5 and  a_(n)=4a_(n-1)-5  a_(1)=5 and  a_(n)=-5a_(n-1)+4  a_(1)=5 and  a_(n)=-4a_(n-1)-1

Bytelearn · Accepted Answer

Identify First Term: Identify the first term of the sequence. The first term given is a_(1) = 5. This is the starting point for our recursive sequence.Find Pattern: Use the second term to find a pattern. The second term is -21. We need to find a recursive formula that, when applied to the first term (5), gives us the second term (-21).Test First Formula: Test the first given recursive formula. a_(1) = 5 and a_(n) = -a_(n-1) - 4 Apply it to find the second term: a_(2) = -a_(1) - 4 = -5 - 4 = -9 This does not match the second term of the sequence (-21), so this formula is incorrect.Test Second Formula: Test the second given recursive formula. a_(1) = 5 and a_(n) = 4a_(n-1) - 5 Apply it to find the second term: a_(2) = 4a_(1) - 5 = 4*5 - 5 = 20 - 5 = 15 This does not match the second term of the sequence (-21), so this formula is also incorrect.Test Third Formula: Test the third given recursive formula. a_(1) = 5 and a_(n) = -5a_(n-1) + 4 Apply it to find the second term: a_(2) = -5a_(1) + 4 = -5*5 + 4 = -25 + 4 = -21 This matches the second term of the sequence (-21), so this formula could be correct. Let's test it with the third term.Verify Third Term: Verify the third term with the third recursive formula. The third term is 109. Apply the formula to find the third term: a_(3) = -5a_(2) + 4 = -5*(-21) + 4 = 105 + 4 = 109 This matches the third term of the sequence (109), so this formula is correct.Test Fourth Formula: Test the fourth given recursive formula as a formality. a_(1) = 5 and a_(n) = -4a_(n-1) - 1 Apply it to find the second term: a_(2) = -4a_(1) - 1 = -4*5 - 1 = -20 - 1 = -21 This matches the second term of the sequence (-21), but we need to check the third term to be sure.Verify Third Term: Verify the third term with the fourth recursive formula. Apply the formula to find the third term: a_(3) = -4a_(2) - 1 = -4*(-21) - 1 = 84 - 1 = 83 This does not match the third term of the sequence (109), so this formula is incorrect.

Which recursive sequence would produce the sequence $5,-21,109, \ldots$ ? $\newline$ $a_{1}=5$ and $a_{n}=-a_{n-1}-4$ $\newline$ $a_{1}=5$ and $a_{n}=4 a_{n-1}-5$ $\newline$ $a_{1}=5$ and $a_{n}=-5 a_{n-1}+4$ $\newline$ $a_{1}=5$ and $a_{n}=-4 a_{n-1}-1$

Full solution

More problems from Identify a sequence as explicit or recursive

Related topics