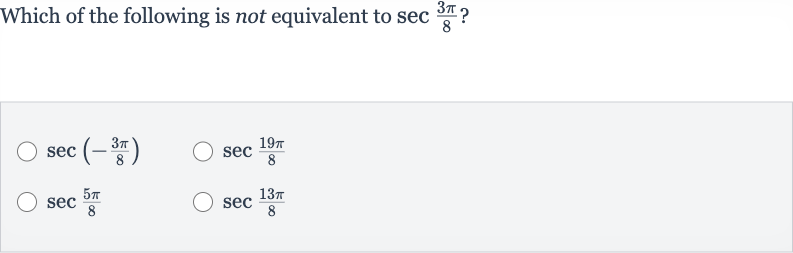
Which of the following is not equivalent to sec ((3pi)/(8)) ? sec(-(3pi)/(8)) sec ((19 pi)/(8)) sec ((5pi)/(8)) sec ((13 pi)/(8))

Question

Which of the following is not equivalent to  sec ((3pi)/(8)) ?  sec(-(3pi)/(8))  sec ((19 pi)/(8))  sec ((5pi)/(8))  sec ((13 pi)/(8))

Bytelearn · Accepted Answer

Secant Function Properties: Understand the properties of the secant function. The secant function, sec(θ), is periodic with a period of 2π. This means that sec(θ) = sec(θ + 2πn) for any integer n. Also, sec(-θ) = sec(θ) because secant is an even function.Evaluate -(3pi)/(8): Evaluate sec(-(3pi)/(8)). Using the property that secant is an even function, we have sec(-(3pi)/(8)) = sec((3pi)/(8)).Evaluate (19pi)/(8): Evaluate sec((19pi)/(8)). Since the secant function has a period of 2π, we can subtract 2π (which is the same as subtracting (16pi)/(8)) from (19pi)/(8) to find an equivalent angle in the range of one period. So, sec((19pi)/(8)) = sec((19pi)/(8) - (16pi)/(8)) = sec((3pi)/(8)).Evaluate (5pi)/(8): Evaluate sec((5pi)/(8)). The angle (5pi)/(8) is not a simple transformation of (3pi)/(8) by adding or subtracting full periods (2π), nor is it the negative of (3pi)/(8). Therefore, we need to consider if this angle is equivalent to (3pi)/(8) by other means. However, (5pi)/(8) is not an equivalent angle to (3pi)/(8) because they are in different quadrants of the unit circle, and secant values are different in different quadrants unless the angles are related by a full period.Evaluate (13pi)/(8): Evaluate sec((13pi)/(8)). We can subtract 2π from (13pi)/(8) to find an equivalent angle. So, sec((13pi)/(8)) = sec((13pi)/(8) - (16pi)/(8)) = sec(-(3pi)/(8)). As we established in Step 2, sec(-(3pi)/(8)) = sec((3pi)/(8)).Identify Non-Equivalent Option: Determine which option is not equivalent. From the previous steps, we have established that sec(-(3pi)/(8)), sec((19pi)/(8)), and sec((13pi)/(8)) are all equivalent to sec((3pi)/(8)). Therefore, the option that is not equivalent to sec((3pi)/(8)) is sec((5pi)/(8)).

Which of the following is not equivalent to $\sec \frac{3 \pi}{8}$ ? $\newline$ $\sec \left(-\frac{3 \pi}{8}\right)$ $\newline$ $\sec \frac{19 \pi}{8}$ $\newline$ $\sec \frac{5 \pi}{8}$ $\newline$ $\sec \frac{13 \pi}{8}$

Full solution

More problems from Multiplication with rational exponents

Related topics