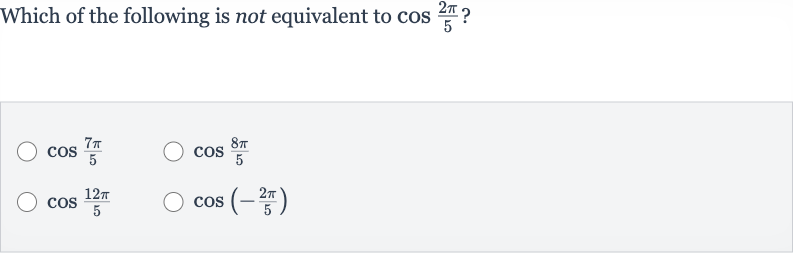
Which of the following is not equivalent to cos ((2pi)/(5)) ? cos ((7pi)/(5)) cos ((8pi)/(5)) cos ((12 pi)/(5)) cos(-(2pi)/(5))

Question

Which of the following is not equivalent to  cos ((2pi)/(5)) ?  cos ((7pi)/(5))  cos ((8pi)/(5))  cos ((12 pi)/(5))  cos(-(2pi)/(5))

Bytelearn · Accepted Answer

Properties of Cosine Function: Understand the properties of the cosine function. The cosine function is periodic with a period of 2π, which means cos(θ) = cos(θ + 2πn) for any integer n. Also, cosine is an even function, so cos(θ) = cos(-θ).Evaluate cos ((7pi)/(5)): Evaluate cos ((7pi)/(5)). Using the periodic property of cosine, we can subtract 2π from (7π/5) to find an equivalent angle within the range of 0 to 2π. cos ((7pi)/(5)) = cos ((7pi)/(5) - 2π) = cos ((7pi)/(5) - (10π/5)) = cos ((-3π)/(5)) Since cosine is an even function, cos ((-3π)/(5)) = cos ((3π)/(5)). Now, (3π/5) is not equivalent to (2π/5), so cos ((7pi)/(5)) is not equivalent to cos ((2pi)/(5)).Evaluate cos ((8pi)/(5)): Evaluate cos ((8pi)/(5)). Using the periodic property of cosine, we can subtract 2π from (8π/5) to find an equivalent angle within the range of 0 to 2π. cos ((8pi)/(5)) = cos ((8pi)/(5) - 2π) = cos ((8pi)/(5) - (10π/5)) = cos ((-2π)/(5)) Since cosine is an even function, cos ((-2π)/(5)) = cos ((2π)/(5)). Therefore, cos ((8pi)/(5)) is equivalent to cos ((2pi)/(5)).Evaluate cos ((12pi)/(5)): Evaluate cos ((12pi)/(5)). Using the periodic property of cosine, we can subtract 2π from (12π/5) multiple times until we find an equivalent angle within the range of 0 to 2π. cos ((12pi)/(5)) = cos ((12pi)/(5) - 2π) = cos ((12pi)/(5) - (10π/5)) = cos ((2π)/(5)) Therefore, cos ((12pi)/(5)) is equivalent to cos ((2pi)/(5)).Evaluate cos (-(2pi)/(5)): Evaluate cos (-(2pi)/(5)). Since cosine is an even function, cos (-(2pi)/(5)) = cos ((2pi)/(5)). Therefore, cos (-(2pi)/(5)) is equivalent to cos ((2pi)/(5)).

Which of the following is not equivalent to $\cos \frac{2 \pi}{5}$ ? $\newline$ $\cos \frac{7 \pi}{5}$ $\newline$ $\cos \frac{8 \pi}{5}$ $\newline$ $\cos \frac{12 \pi}{5}$ $\newline$ $\cos \left(-\frac{2 \pi}{5}\right)$

Full solution

More problems from Multiplication with rational exponents

Related topics