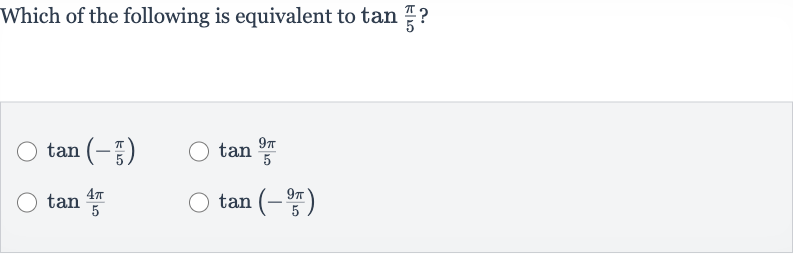AI tutor
Full solution
Q. Which of the following is equivalent to ?
- Periodicity of Tangent Function: Understand the periodicity of the tangent function. The tangent function has a period of , which means that for any integer .
- Comparison with Original Angle: Compare the given angles with the original angle using the periodicity of the tangent function.We need to find an angle that differs from by an integer multiple of .
- Analysis: : Analyze the first option: . The tangent function is odd, which means . Therefore, is not equivalent to because it will have the opposite sign.
- Analysis: : Analyze the second option: . Using the periodicity of the tangent function, we can subtract from to see if it is equivalent to . . This is not equivalent to .
- Analysis: : Analyze the third option: . This angle is not equivalent to because it is not an integer multiple of away from .
- Analysis: : Analyze the fourth option: . Using the periodicity of the tangent function, we can add to to see if it is equivalent to . . This is not equivalent to because it is not an integer multiple of away from .
- Conclusion: Conclusion.None of the given options are equivalent to because none of them are an integer multiple of away from .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help