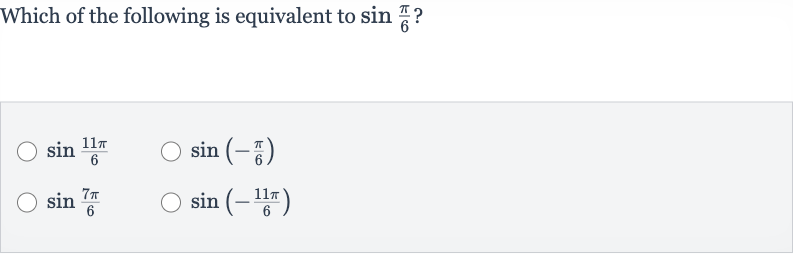
Which of the following is equivalent to sin ((pi)/(6)) ? sin ((11 pi)/(6)) sin(-(pi)/(6)) sin ((7pi)/(6)) sin(-(11 pi)/(6))

Question

Which of the following is equivalent to  sin ((pi)/(6)) ?  sin ((11 pi)/(6))  sin(-(pi)/(6))  sin ((7pi)/(6))  sin(-(11 pi)/(6))

Bytelearn · Accepted Answer

Properties of Sine Function: Understand the properties of the sine function. The sine function has a period of 2π, which means sin(θ) = sin(θ + 2πk) for any integer k. Also, sin(θ) = sin(π - θ) and sin(θ) = -sin(-θ).Evaluate sin((pi)/(6)): Evaluate sin((pi)/(6)). We know that sin((pi)/(6)) is equal to 1/2 because (pi)/(6) is 30 degrees, and the sine of 30 degrees is 1/2.Compare sin((pi)/(6)) with sin((11pi)/(6)): Compare sin((pi)/(6)) with sin((11pi)/(6)). Using the periodic property, sin((11pi)/(6)) is the same as sin((11pi)/(6) - 2π) because subtracting 2π is equivalent to completing one full circle on the unit circle. So, sin((11pi)/(6)) = sin((11pi)/(6) - 2π) = sin((-pi)/(6)). Since sin(θ) = -sin(-θ), sin((-pi)/(6)) = -sin((pi)/(6)). Therefore, sin((11pi)/(6)) is not equivalent to sin((pi)/(6)).Compare sin((pi)/(6)) with sin(-(pi)/(6)): Compare sin((pi)/(6)) with sin(-(pi)/(6)). Using the property sin(θ) = -sin(-θ), we have sin(-(pi)/(6)) = -sin((pi)/(6)). Therefore, sin(-(pi)/(6)) is not equivalent to sin((pi)/(6)).Compare sin((pi)/(6)) with sin((7pi)/(6)): Compare sin((pi)/(6)) with sin((7pi)/(6)). Using the periodic property, sin((7pi)/(6)) is the same as sin((7pi)/(6) - 2π) = sin((-5pi)/(6)). Since sin(θ) = -sin(-θ), sin((-5pi)/(6)) = -sin((5pi)/(6)). And since sin(θ) = sin(π - θ), sin((5pi)/(6)) = sin(π - (5pi)/(6)) = sin((pi)/(6)). Therefore, sin((7pi)/(6)) is not equivalent to sin((pi)/(6)) because of the negative sign.Compare sin((pi)/(6)) with sin(-(11pi)/(6)): Compare sin((pi)/(6)) with sin(-(11pi)/(6)). Using the periodic property, sin(-(11pi)/(6)) is the same as sin(-(11pi)/(6) + 2π) = sin((pi)/(6)). Therefore, sin(-(11pi)/(6)) is equivalent to sin((pi)/(6)).

Which of the following is equivalent to $\sin \frac{\pi}{6}$ ? $\newline$ $\sin \frac{11 \pi}{6}$ $\newline$ $\sin \left(-\frac{\pi}{6}\right)$ $\newline$ $\sin \frac{7 \pi}{6}$ $\newline$ $\sin \left(-\frac{11 \pi}{6}\right)$

Full solution

More problems from Multiplication with rational exponents

Related topics