Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which expressions are equivalent to (root(4)(x))^(-1) ? Choose all answers that apply: A x^(-4) B (sqrtx)^(-4) c -root(4)(x) D None of the above

Which expressions are equivalent to (x4)−1 (\sqrt[4]{x})^{-1} ?\newlineChoose all answers that apply:\newlineA x−4 x^{-4} \newlineB (x)−4 (\sqrt{x})^{-4} \newlinec −x4 -\sqrt[4]{x} \newlineD None of the above

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 7right chevron icon
Identify equivalent linear expressions Iright chevron icon

Full solution

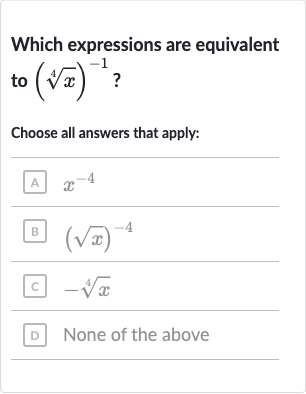
Q. Which expressions are equivalent to (x4)−1 (\sqrt[4]{x})^{-1} ?\newlineChoose all answers that apply:\newlineA x−4 x^{-4} \newlineB (x)−4 (\sqrt{x})^{-4} \newlinec −x4 -\sqrt[4]{x} \newlineD None of the above
  1. Step 11: Understand the expression: Understand the expression (x4)−1(\sqrt[4]{x})^{-1}. The expression represents the fourth root of xx, raised to the power of −1-1. This means we are looking for the reciprocal of the fourth root of xx.
  2. Step 22: Simplify the expression: Simplify the expression using the properties of exponents.\newlineThe reciprocal of a number is the same as raising that number to the power of −1-1. Therefore, (x4)−1(\sqrt[4]{x})^{-1} is the same as x−14x^{-\frac{1}{4}}.
  3. Step 33: Compare with given choices: Compare the simplified expression with the given choices.\newlineA. x(−4)x^{(-4)} is not equivalent because it represents xx raised to the power of −4-4, not −14-\frac{1}{4}.\newlineB. (x)(−4)(\sqrt{x})^{(-4)} is not equivalent because it represents the square root of xx raised to the power of −4-4, which is x(−2)x^{(-2)}, not x(−14)x^{(-\frac{1}{4})}.\newlineC. −x4-\sqrt[4]{x} is not equivalent because it represents the negative fourth root of xx, not the reciprocal of the fourth root of xx.\newlineD. None of the above is the correct choice because none of the given options match x(−14)x^{(-\frac{1}{4})}.

More problems from Identify equivalent linear expressions I

Question
Simplify the expression:\newline7z2+3z27z^2 + 3z^2 \newline ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify the expression:\newline10f+8f−9f−6f10f + 8f - 9f - 6f\newline____
Get tutor helpright-arrow

Posted 2 months ago

Question
Subtract.\newline(3h+6)−(3h+2)(3h + 6) - (3h + 2)\newline____
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify the expression:\newline2p−p2p - p \newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
A school charges $6\$6 per ticket to a dance. They spend $300\$300 on music and decorations. The expression 6n−3006n-300 describes the amount of profit the school makes from the dance if nn students buy tickets. What does 6n6n represent in this context?\newlineChoices:\newline(A)The amount of money the school charges for all `\n` tickets\newline(B)The amount of money the school spends on the dance\newline(C)The number of students who buy tickets\newline(D)The profit the school earns per ticket
Get tutor helpright-arrow

Posted 3 months ago

Question
Which is equal to cos⁡60∘ \cos 60^\circ ? \newlineChoices:\newline(A) sin⁡30∘ \sin 30^\circ \newline(B) sin⁡60∘ \sin 60^\circ \newline(C) cos⁡30∘ \cos 30^\circ \newline(D) cos⁡60∘ \cos 60^\circ
Get tutor helpright-arrow

Posted 4 months ago

Question
Which is equal to sin⁡45∘\sin 45^\circ? \newlineChoices:\newline(A) cos⁡45∘\cos 45^\circ\newline(B) cos⁡55∘\cos 55^\circ\newline(C) sin⁡55∘\sin 55^\circ\newline(D) sin⁡35∘\sin 35^\circ
Get tutor helpright-arrow

Posted 2 months ago

Question
Which is equal to cos⁡75∘\cos 75^\circ? \newlineChoices:\newline(A) sin⁡15∘\sin 15^\circ\newline(B) sin⁡75∘\sin 75^\circ\newline(C) cos⁡15∘\cos 15^\circ\newline(D) cos⁡25∘\cos 25^\circ
Get tutor helpright-arrow

Posted 2 months ago

Question
Which is equal to sin⁡30∘ \sin 30^\circ ? \newlineChoices:\newline(A) cos⁡60∘ \cos 60^\circ \newline(B) cos⁡30∘ \cos 30^\circ \newline(C) sin⁡60∘ \sin 60^\circ \newline(D) sin⁡30∘ \sin 30^\circ
Get tutor helpright-arrow

Posted 2 months ago

Question
Which is equal to cos⁡45∘ \cos 45^\circ ? \newlineChoices:\newline(A) sin⁡45∘ \sin 45^\circ \newline(B) sin⁡55∘ \sin 55^\circ \newline(C) cos⁡55∘ \cos 55^\circ \newline(D) cos⁡35∘ \cos 35^\circ
Get tutor helpright-arrow

Posted 2 months ago

View all (166)