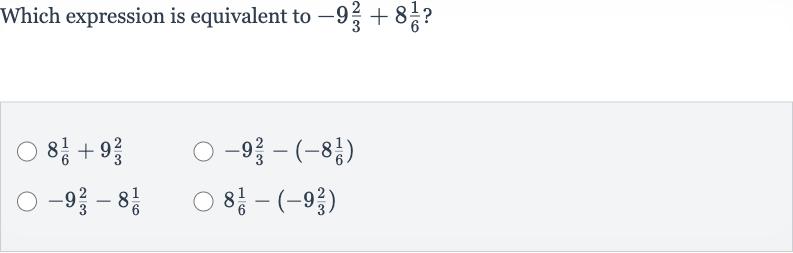AI tutor
Full solution
Q. Which expression is equivalent to ?
- Convert to Improper Fractions: First, let's convert the mixed numbers to improper fractions. becomes which is . becomes which is .
- Addition of Fractions: Now, let's look at the first option: . Convert to improper fractions: . To add these, we need a common denominator.
- Subtraction of Fractions: The common denominator for and is . So, convert to . Now we have . This is not equivalent to our original expression.
- Common Denominator: Next, let's look at the second option: . Convert to improper fractions: . We need a common denominator again.
- Final Comparison: The common denominator is . Convert to . Now we have . This simplifies to , which is not equivalent to our original expression.
- Final Comparison: The common denominator is . Convert to . Now we have . This simplifies to , which is not equivalent to our original expression.Now, let's look at the third option: . We already have the improper fractions: and . We need a common denominator.
- Final Comparison: The common denominator is . Convert to . Now we have . This simplifies to , which is not equivalent to our original expression. Now, let's look at the third option: . We already have the improper fractions: and . We need a common denominator. The common denominator is . Convert to . Now we have . This is equivalent to our original expression.
- Final Comparison: The common denominator is . Convert to . Now we have . This simplifies to , which is not equivalent to our original expression. Now, let's look at the third option: . We already have the improper fractions: and . We need a common denominator. The common denominator is . Convert to . Now we have . This is equivalent to our original expression. Lastly, let's look at the fourth option: . Convert to improper fractions: . We need a common denominator.
- Final Comparison: The common denominator is . Convert to . Now we have . This simplifies to , which is not equivalent to our original expression. Now, let's look at the third option: . We already have the improper fractions: and . We need a common denominator. The common denominator is . Convert to . Now we have . This is equivalent to our original expression. Lastly, let's look at the fourth option: . Convert to improper fractions: . We need a common denominator. The common denominator is . Convert to . Now we have . This is not equivalent to our original expression.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help