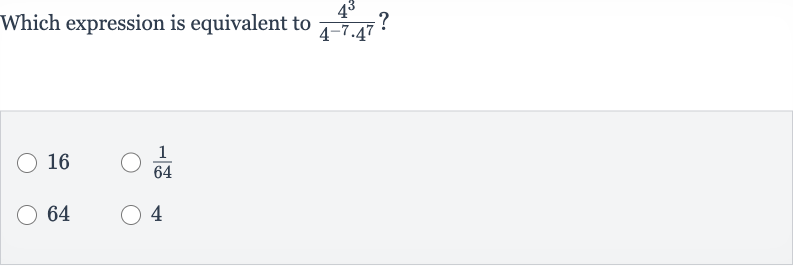AI tutor
Full solution
Q. Which expression is equivalent to
- Simplify Expression: Simplify the expression using the properties of exponents.We have the expression . According to the properties of exponents, when we divide powers with the same base, we subtract the exponents. When we multiply powers with the same base, we add the exponents.
- Apply Exponent Properties: Apply the properties of exponents to the denominator.First, we'll simplify the denominator by adding the exponents of the terms with the same base:Since any number raised to the power of is , we have:
- Divide Numerator by Denominator: Divide the numerator by the denominator.Now we divide by , which is simply since any number divided by is the number itself:
- Calculate : Calculate the value of . means multiplied by itself times:
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help