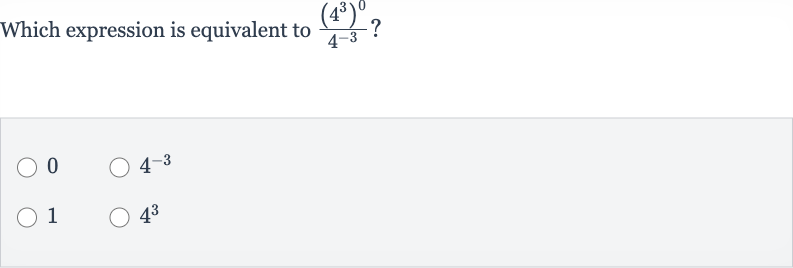AI tutor
Full solution
Q. Which expression is equivalent to
- Simplify numerator: Simplify the numerator . Any number raised to the power of is . Therefore, .
- Simplify denominator: Simplify the denominator . A negative exponent means that the base is on the wrong side of the fraction line, so we take the reciprocal of the base and make the exponent positive. Therefore, .
- Write expression: Write the expression after simplifying the numerator and the denominator.We have for the numerator from Step and for the denominator from Step .So, the expression becomes .
- Simplify final expression: Simplify the expression . When dividing by a fraction, it is equivalent to multiplying by its reciprocal. Therefore, .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help