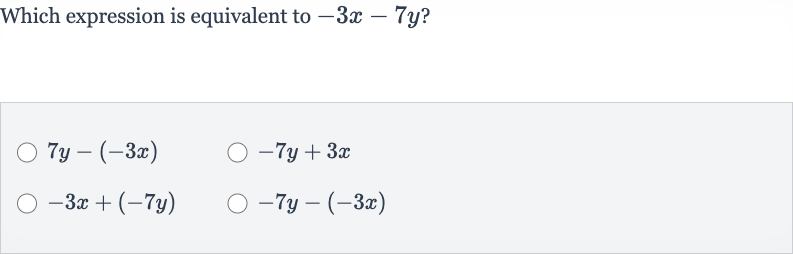Which expression is equivalent to -3x-7y ? 7y-(-3x) -7y+3x -3x+(-7y) -7y-(-3x)

Question

Which expression is equivalent to  -3x-7y ?  7y-(-3x)  -7y+3x  -3x+(-7y)  -7y-(-3x)

Bytelearn · Accepted Answer

Understand the problem: Understand the problem. We need to find the expression that is equivalent to -3x - 7y. This means we are looking for an expression that has the same terms and coefficients as -3x - 7y.Compare expressions: Compare the given expressions with -3x - 7y. We will compare each expression one by one to see if they are equivalent to -3x - 7y.  Expression A: 7y - (-3x) This expression can be simplified by removing the parentheses and changing the sign of the term inside the parentheses, which gives us 7y + 3x. This is not equivalent to -3x - 7y because the signs of the terms are different.Check Expression A: Check the second expression. Expression B: -7y + 3x This expression has the same coefficients as -3x - 7y but the terms are in reverse order and the sign of the first term is different. This is not equivalent to -3x - 7y because the sign of the y term is different.Check Expression B: Check the third expression. Expression C: -3x + (-7y) This expression is the same as -3x - 7y because adding a negative is the same as subtracting. Therefore, this expression is equivalent to -3x - 7y.Check Expression C: Check the fourth expression. Expression D: -7y - (-3x) This expression can be simplified by removing the parentheses and changing the sign of the term inside the parentheses, which gives us -7y + 3x. This is not equivalent to -3x - 7y because the signs of the terms are different.

Which expression is equivalent to $-3 x-7 y$ ? $\newline$ $7 y-(-3 x)$ $\newline$ $-7 y+3 x$ $\newline$ $-3 x+(-7 y)$ $\newline$ $-7 y-(-3 x)$

Full solution

More problems from Simplify variable expressions involving like terms and the distributive property

Related topics

Which expression is equivalent to −3x−7y -3 x-7 y −3x−7y ?\newline7y−(−3x) 7 y-(-3 x) 7y−(−3x)\newline−7y+3x -7 y+3 x −7y+3x\newline−3x+(−7y) -3 x+(-7 y) −3x+(−7y)\newline−7y−(−3x) -7 y-(-3 x) −7y−(−3x)

Which expression is equivalent to $-3 x-7 y$ ? $\newline$ $7 y-(-3 x)$ $\newline$ $-7 y+3 x$ $\newline$ $-3 x+(-7 y)$ $\newline$ $-7 y-(-3 x)$