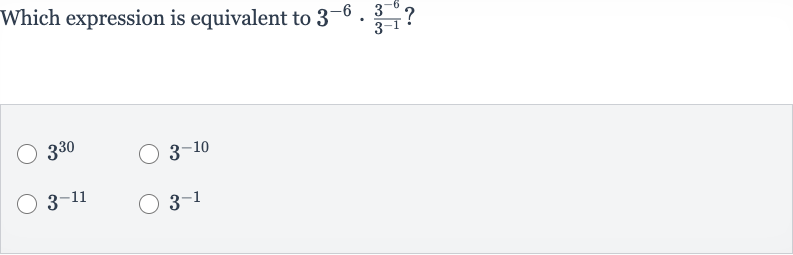AI tutor
Full solution
Q. Which expression is equivalent to
- Write and Apply Exponent Rules: Write down the given expression and apply the exponent rules.The expression given is .When multiplying with the same base, we add the exponents. When dividing with the same base, we subtract the exponents.
- Add Exponents for Multiplication: Add the exponents for the multiplication part of the expression..
- Subtract Exponent for Division: Subtract the exponent for the division part of the expression.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help