Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which expression is equivalent to
(3^(2)×3^(-1))^(2) ?
9

(1)/(9)
81
27

Which expression is equivalent to $\left(3^{2} \times 3^{-1}\right)^{2}$ ? $\newline$ $9$ $\newline$ $\frac{1}{9}$ $\newline$ $81$ $\newline$ $27$

View step-by-step help

View step-by-step help

Simplify radical expressions with root inside the root

Full solution

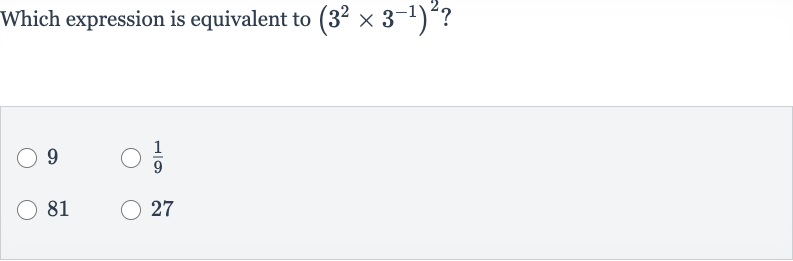
Q. Which expression is equivalent to

\left(3^{2} \times 3^{-1}\right)^{2}

?

\newline

9

\newline

\frac{1}{9}

\newline

81

\newline

27

Simplify Exponents Using Properties: Simplify the expression inside the parentheses using the properties of exponents. $\newline$ The property of exponents we will use is that when we multiply powers with the same base, we add the exponents: $a^m \times a^n = a^{m+n}$ . $\newline$ $(3^{2}\times3^{-1}) = 3^{2-1} = 3^{1}$
Apply Power to Power Rule: Apply the power to a power rule to the simplified expression. $\newline$ The power to a power rule states that $(a^m)^n = a^{m*n}$ . $\newline$ $(3^{1})^{2} = 3^{1*2} = 3^{2}$
Calculate Final Value: Calculate the final value of the expression. $3^{2} = 3 \times 3 = 9$

More problems from Simplify radical expressions with root inside the root

Question

Find the real-number root.

\newline

\sqrt{16}

\newline

\newline

Write your answer in simplified form.

\newline

\_\_\_\_

Posted 3 months ago

Question

Find the real-number root.

\newline

\sqrt{\frac{9}{16}}

\newline

Simplify your answer and write it as a decimal or as a proper or improper fraction.

\newline

\_\_\_\_\_

Posted 3 months ago

Question

Find the real-number root using a calculator. Round your answer to the nearest thousandth.

\newline

\newline

Posted 3 months ago

Question

Multiply. Write your answer in simplest form.

\newline

\sqrt{273} \times \sqrt{42}

\newline

Posted 1 month ago

Question

\newline

\sqrt{\frac{63}{4}}

\newline

Posted 3 months ago

Question

Simplify. Rationalize the denominator.

\newline

\frac{-4}{9 - \sqrt{2}}

\newline

Posted 3 months ago

Question

z

\newline

16 = \sqrt{z}

\newline

z =

Posted 3 months ago

Question

Simplify the radical expression.

\sqrt{14x^{14}}

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

Posted 3 months ago

Question

Simplify the radical expression.

\newline

\sqrt{12x^{12}}

\newline

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

\newline

\underline{\hspace{3cm}}

Posted 3 months ago

Question

What is the value of

\sin \left(\frac{5 \pi}{6}\right) ?

\newline

1

\newline

-\frac{\sqrt{3}}{2}

\newline

-\frac{\sqrt{2}}{2}

\newline

\frac{1}{2}

\newline

150

Posted 4 months ago