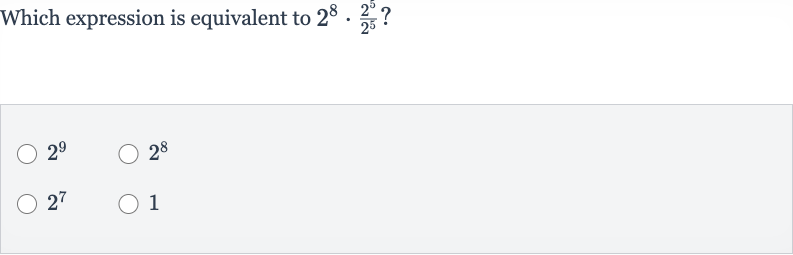AI tutor
Full solution
Q. Which expression is equivalent to
- Simplify Exponents: Simplify the expression using the properties of exponents.We have the expression . According to the properties of exponents, when we divide two expressions with the same base, we subtract the exponents.So, .
- Simplify Division: Simplify the division part of the expression.Since is equal to (because any number divided by itself is ), we can simplify the expression further..
- Multiply Result: Multiply by .Multiplying any number by does not change the number, so is simply .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help