AI tutor
Full solution
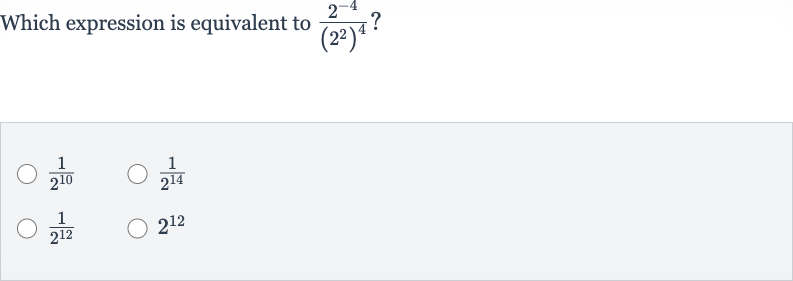
Q. Which expression is equivalent to
- Simplify Denominator: Simplify the denominator.The denominator is , which is a power of a power. According to the rules of exponents, when you raise a power to a power, you multiply the exponents.
- Rewrite Expression: Rewrite the original expression with the simplified denominator.Now we have the expression .
- Apply Quotient Rule: Apply the quotient rule for exponents.When dividing like bases with exponents, you subtract the exponents.
- Convert Negative Exponent: Convert the negative exponent to a positive exponent.A negative exponent means that the base is on the wrong side of the fraction line. To make the exponent positive, we can rewrite the expression as over the base raised to the positive exponent.
- Compare with Options: Compare the result with the given options.The expression matches one of the given options, which is .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help