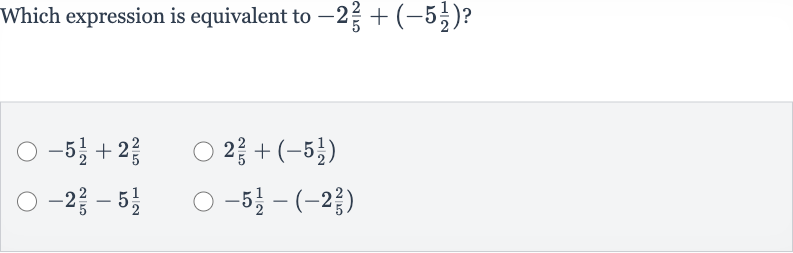Which expression is equivalent to -2(2)/(5)+(-5(1)/(2)) ? -5(1)/(2)+2(2)/(5) 2(2)/(5)+(-5(1)/(2)) -2(2)/(5)-5(1)/(2) -5(1)/(2)-(-2(2)/(5))

Question

Which expression is equivalent to  -2(2)/(5)+(-5(1)/(2)) ?  -5(1)/(2)+2(2)/(5)  2(2)/(5)+(-5(1)/(2))  -2(2)/(5)-5(1)/(2)  -5(1)/(2)-(-2(2)/(5))

Bytelearn · Accepted Answer

Understand the problem: Understand the problem. We need to find the expression equivalent to the given expression -2(2)/(5)+(-5(1)/(2)). This involves adding two fractions with different denominators.Identify the denominators: Identify the denominators of the fractions. The denominators of the given fractions are 5 and 2. To add these fractions, we need a common denominator.Find the LCD: Find the least common denominator (LCD). The LCD of 5 and 2 is 10 because it is the smallest number that both 5 and 2 can divide into without leaving a remainder.Convert to equivalent fractions: Convert each fraction to an equivalent fraction with the LCD as the denominator. -2(2)/(5) becomes -2(2)*(2)/(5*2) = -4(4)/(10) (-5(1)/(2)) becomes (-5(1))*(5)/(2*5) = -5(5)/(10)Add equivalent fractions: Add the equivalent fractions. -4(4)/(10) + (-5(5)/(10)) = (-4(4) - 5(5))/(10)Perform addition in numerator: Perform the addition in the numerator. -4(4) - 5(5) = -8 - 25 = -33Write final expression: Write the final expression. The final expression is -33/10, which is equivalent to -3(3)/(10) or -3.3.Match with given options: Match the final expression with the given options. The final expression -33/10 or -3(3)/(10) is not explicitly listed in the options. However, we can see that the option ＂-2(2)/(5)-5(1)/(2)＂ is the original expression with a different sign between the terms. Since we have not changed the signs of the terms, this option cannot be equivalent to the original expression. The correct equivalent expression must have the same terms with the same signs, so the equivalent expression is ＂-2(2)/(5)+(-5(1)/(2))＂.

Which expression is equivalent to $-2 \frac{2}{5}+\left(-5 \frac{1}{2}\right)$ ? $\newline$ $-5 \frac{1}{2}+2 \frac{2}{5}$ $\newline$ $2 \frac{2}{5}+\left(-5 \frac{1}{2}\right)$ $\newline$ $-2 \frac{2}{5}-5 \frac{1}{2}$ $\newline$ $-5 \frac{1}{2}-\left(-2 \frac{2}{5}\right)$

Full solution

More problems from Multiplication with rational exponents

Related topics