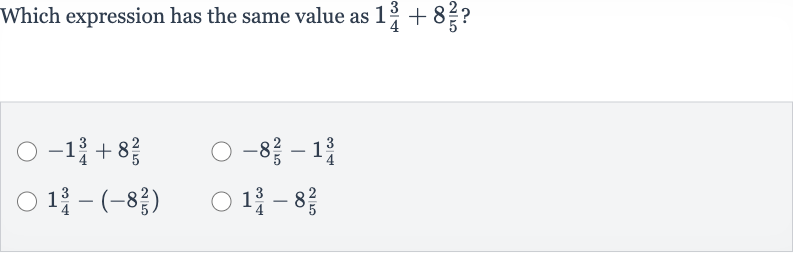AI tutor
Full solution
Q. Which expression has the same value as ?
- Understand the problem: Understand the problem.We need to find the expression that has the same value as the given expression . This involves addition of mixed numbers.
- Convert to improper fractions: Convert mixed numbers to improper fractions. can be converted to an improper fraction by multiplying the whole number by the denominator and adding the numerator: . can be converted to an improper fraction by multiplying the whole number by the denominator and adding the numerator: .
- Add fractions with common denominator: Add the improper fractions.Since the denominators are different, we cannot add the fractions directly. We need to find a common denominator. The least common multiple of and is .
- Convert back to mixed number: Convert the fractions to have a common denominator. can be converted to a fraction with a denominator of by multiplying both the numerator and denominator by : . can be converted to a fraction with a denominator of by multiplying both the numerator and denominator by : .
- Compare the expressions: Add the fractions with the common denominator.Now we can add the fractions: .
- Compare the expressions: Add the fractions with the common denominator.Now we can add the fractions: .Convert the improper fraction back to a mixed number. can be converted to a mixed number by dividing the numerator by the denominator: with a remainder of . So the mixed number is . Since can be simplified further, we divide both the numerator and denominator by their greatest common divisor, which is , so the fraction remains the same.
- Compare the expressions: Add the fractions with the common denominator.Now we can add the fractions: .Convert the improper fraction back to a mixed number. can be converted to a mixed number by dividing the numerator by the denominator: with a remainder of . So the mixed number is . Since can be simplified further, we divide both the numerator and denominator by their greatest common divisor, which is , so the fraction remains the same.Compare the expressions.The original expression is equal to . Now we need to find which of the given options is equivalent to this value.- changes the sign of the first term, so it cannot be equivalent.- changes the sign of both terms and the order, so it cannot be equivalent. is equivalent because subtracting a negative is the same as adding a positive, which matches the original expression. changes the operation from addition to subtraction, so it cannot be equivalent.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help