Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which exponential expression is equivalent to
root(9)(z) ?
Choose 1 answer:
(A)
z^(9)
(B)
(1)/(z^((1)/(9)))
(C)
(1)/(z^(9))
(D)
z^((1)/(9))

Which exponential expression is equivalent to $\sqrt[9]{z}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $z^{9}$ $\newline$ (B) $\frac{1}{z^{\frac{1}{9}}}$ $\newline$ (C) $\frac{1}{z^{9}}$ $\newline$ (D) $z^{\frac{1}{9}}$

View step-by-step help

View step-by-step help

Identify equivalent linear expressions

Full solution

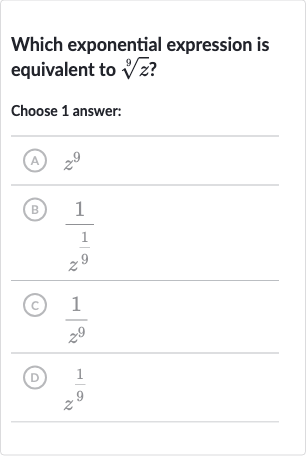
Q. Which exponential expression is equivalent to

\sqrt[9]{z}

?

\newline

Choose

1

answer:

\newline

(A)

z^{9}

\newline

(B)

\frac{1}{z^{\frac{1}{9}}}

\newline

(C)

\frac{1}{z^{9}}

\newline

(D)

z^{\frac{1}{9}}

Express $9$ th Root as Exponent: We need to express the $9$ th root of $z$ as an exponent. The $9$ th root of a number is the same as raising that number to the power of $\frac{1}{9}$ .
Write Expression for $9$ th Root of z: The expression for the $9$ th root of $z$ can be written as $z^{1/9}$ . This is because in general, the $n$ th root of a number $x$ is $x^{1/n}$ .
Analyze Given Options: Now we look at the options given to find which one matches our expression $z^{\frac{1}{9}}$ .
(A) $z^{9}$ is incorrect because it represents $z$ raised to the $9^{\text{th}}$ power, not the $9^{\text{th}}$ root of $z$ .
(B) $\frac{1}{z^{\frac{1}{9}}}$ is incorrect because it represents the reciprocal of the $9^{\text{th}}$ root of $z$ .
(C) $\frac{1}{z^{9}}$ is incorrect because it represents the reciprocal of $z$ raised to the $9^{\text{th}}$ power.
(D) $z^{\frac{1}{9}}$ is correct because it represents the $9^{\text{th}}$ root of $z$ .
Identify Correct Answer: The correct answer is (D) $z^{\frac{1}{9}}$ , which is equivalent to the $9$ th root of $z$ .

More problems from Identify equivalent linear expressions

Question

Evaluate the expression for

j = 7

\newline

2j =

Posted 2 months ago

Question

Evaluate the expression for

y = 4

z = 5

\newline

yz =

Posted 1 month ago

Question

Evaluate the expression for

t = 0

\newline

|-4 - t| =

Posted 2 months ago

Question

8

pictures. Belle drew

p

fewer pictures than Dale. Choose the expression that shows how many pictures Belle drew.

\newline

\newline

8

\newline

p - 8

\newline

8 + p

\newline

8 - p

Posted 2 months ago

Question

Write an expression for the sequence of operations described below. subtract

5

6

w

to the result Do not simplify any part of the expression. ______

Posted 2 months ago

Question

Write an expression for the operation described below.

\newline

4

a

\newline

Posted 2 months ago

Question

12

cookies. Alice baked

n

fewer cookies than John.

\newline

Choose the expression that shows how many cookies Alice baked.

\newline

\newline

12

\newline

n - 12

\newline

12 + n

\newline

12 - n

Posted 3 months ago

Question

15

books. Lucas read

b

fewer books than Emma. Choose the expression that shows how many books Lucas read.

\newline

\newline

15

\newline

b - 15

\newline

15 + b

\newline

15 - b

Posted 3 months ago

Question

10

miles. Sarah ran

m

fewer miles than Max. Choose the expression that shows how many miles Sarah ran.

\newline

\newline

(A)10

\newline

(B)m - 10

\newline

(C)10 + m

\newline

(D)10 - m

Posted 3 months ago

Question

20

poems. Fiona wrote

p

fewer poems than Carlos. Choose the expression that shows how many poems Fiona wrote.

\newline

\newline

20

\newline

p - 20

\newline

20 + p

\newline

20 - p

Posted 3 months ago