Full solution
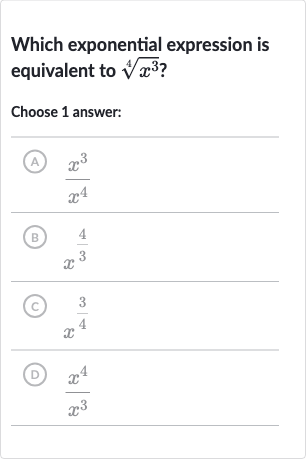
Q. Which exponential expression is equivalent to ?Choose answer:(A) (B) (C) (D)
- Understanding the fourth root: Understand the meaning of the fourth root in terms of exponents.The fourth root of a number is the same as raising that number to the power of .
- Applying the exponent rule: Apply the exponent rule for roots to the given expression.The fourth root of cubed can be written as .
- Using the power of a power rule: Use the power of a power rule.When you raise a power to a power, you multiply the exponents. So, is .
- Performing the multiplication of exponents: Perform the multiplication of the exponents.
- Writing the final expression: Write the final expression.Therefore, the fourth root of cubed is .
More problems from Identify equivalent linear expressions I
QuestionGet tutor help