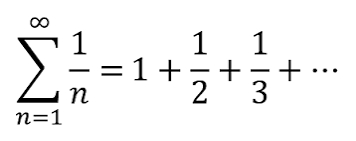AI tutor
Full solution
Q. what is this equal to
- Recognize Nature of Series: The series sum from to of is known as the harmonic series. To determine its value, we need to recognize the nature of this series.
- Harmonic Series Divergence: The harmonic series is a well-known divergent series. This means that as approaches infinity, the sum of the series does not converge to a finite limit; instead, it grows without bound.
- Comparison with Integral: To illustrate the divergence, we can compare the harmonic series to the integral of from to infinity. The integral of from to infinity is equal to the natural logarithm of evaluated from to infinity, which is infinite. Since the integral is a lower bound for the sum of the series, this implies that the harmonic series also diverges to infinity.
- Series Sum Divergence: Therefore, the sum of the series sum from to of does not equal a finite number. Instead, it is said to be divergent or infinite.