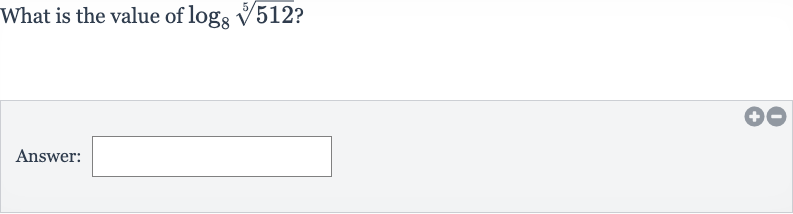
What is the value of log_(8)root(5)(512) ? Answer:

Question

What is the value of  log_(8)root(5)(512) ? Answer:

Bytelearn · Accepted Answer

Identify Value of Fifth Root: Identify the value of the fifth root of 512. The fifth root of a number is the value that, when raised to the power of 5, gives the original number. We know that 512 is 2 raised to the power of 9 (2^9), so we need to find a number that when raised to the power of 5 gives 2^9.Calculate Fifth Root: Calculate the fifth root of 512. Since 512 is 2^9, we can write the fifth root of 512 as (2^9)^(1/5). Using the property of exponents that (a^m)^(1/n) = a^(m/n), we get (2^9)^(1/5) = 2^(9/5) = 2^(1+4/5) = 2 * 2^(4/5).Simplify Expression: Simplify the expression 2 * 2^(4/5). Since 2 is just 2^1, we can combine the exponents by adding them when multiplying the same base. Therefore, 2 * 2^(4/5) = 2^(1+4/5) = 2^(9/5).Rewrite with Simplified Expression: Rewrite the logarithm with the simplified expression. Now we have log base 8 of 2^(9/5). We can use the change of base formula for logarithms, which states that log base a of b = log base c of b / log base c of a. We will use base 2 for this transformation.Apply Change of Base: Apply the change of base formula. Using the change of base formula, we get log base 8 of 2^(9/5) = log base 2 of 2^(9/5) / log base 2 of 8.Simplify Logarithms: Simplify the logarithms. Since the base and the argument of the first logarithm are the same (base 2), log base 2 of 2^(9/5) simplifies to 9/5. For the second logarithm, 8 is 2^3, so log base 2 of 8 simplifies to 3.Complete Division: Complete the division. Now we have (9/5) / 3. To divide a fraction by a whole number, we multiply the fraction by the reciprocal of the whole number. So, (9/5) / 3 = (9/5) * (1/3) = 9/15 = 3/5.Write Final Answer: Write the final answer. The value of log base 8 of the fifth root of 512 is 3/5.

Evaluate. $\newline$ $\log _{8} \sqrt[5]{512}$ $\newline$ Write your answer in simplest form.

Full solution

More problems from Product property of logarithms

Related topics

Evaluate.\newlinelog⁡85125 \log _{8} \sqrt[5]{512} log8​5512​\newlineWrite your answer in simplest form.

Evaluate. $\newline$ $\log _{8} \sqrt[5]{512}$ $\newline$ Write your answer in simplest form.