Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the value of
ln root(4)(e) ?
Answer:

What is the value of $\ln \sqrt[4]{e}$ ? $\newline$ Answer:

View step-by-step help

View step-by-step help

Roots of integers

Full solution

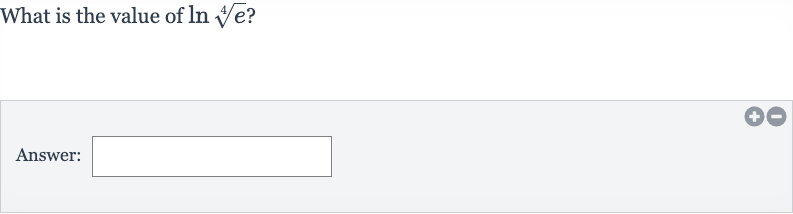
Q. What is the value of

\ln \sqrt[4]{e}

?

\newline

Answer:

Understand the expression: Understand the expression $\ln \sqrt[4]{e}$ . The expression $\ln \sqrt[4]{e}$ means the natural logarithm of the fourth root of $e$ , where $e$ is the base of the natural logarithm, approximately equal to $2.71828$ . The fourth root of a number is the number that, when raised to the power of $4$ , gives the original number. So, we need to find the fourth root of $e$ and then take the natural logarithm of that value.
Calculate the fourth root of $e$ : Calculate the fourth root of $e$ . The fourth root of $e$ can be written as $e^{(1/4)}$ . This is because the $n$ th root of a number can be expressed as that number raised to the power of $1/n$ .
Take the natural logarithm: Take the natural logarithm of the fourth root of $e$ . Since the natural logarithm $\ln(x)$ is the inverse function of the exponential function $e^x$ , we have the property that $\ln(e^x) = x$ . Applying this property to our expression, we get $\ln(e^{1/4}) = \frac{1}{4}$ .

More problems from Roots of integers

Question

Find the real-number root.

\newline

\sqrt{16}

\newline

\newline

Write your answer in simplified form.

\newline

\_\_\_\_

Posted 2 months ago

Question

Find the real-number root.

\newline

\sqrt{\frac{9}{16}}

\newline

Simplify your answer and write it as a decimal or as a proper or improper fraction.

\newline

\_\_\_\_\_

Posted 2 months ago

Question

Find the real-number root using a calculator. Round your answer to the nearest thousandth.

\newline

\newline

Posted 2 months ago

Question

Multiply. Write your answer in simplest form.

\newline

\sqrt{273} \times \sqrt{42}

\newline

Posted 1 month ago

Question

\newline

\sqrt{\frac{63}{4}}

\newline

Posted 2 months ago

Question

Simplify. Rationalize the denominator.

\newline

\frac{-4}{9 - \sqrt{2}}

\newline

Posted 2 months ago

Question

z

\newline

16 = \sqrt{z}

\newline

z =

Posted 2 months ago

Question

Simplify the radical expression.

\sqrt{14x^{14}}

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

Posted 2 months ago

Question

Simplify the radical expression.

\newline

\sqrt{12x^{12}}

\newline

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

\newline

\underline{\hspace{3cm}}

Posted 2 months ago

Question

What is the value of

\sin \left(\frac{5 \pi}{6}\right) ?

\newline

1

\newline

-\frac{\sqrt{3}}{2}

\newline

-\frac{\sqrt{2}}{2}

\newline

\frac{1}{2}

\newline

150

Posted 4 months ago