AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
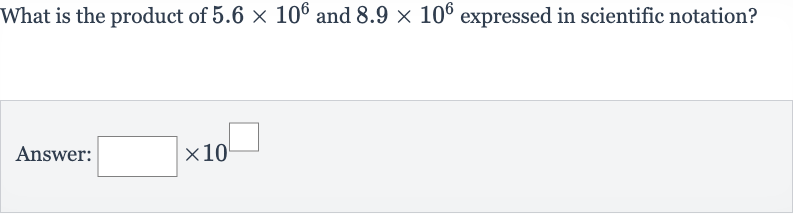
What is the product of and expressed in scientific notation?Answer:
Full solution
Q. What is the product of and expressed in scientific notation?Answer:
- Multiply decimals: Multiply the decimal parts of the numbers.We have and as the decimal parts of the two numbers in scientific notation. To find the product, we multiply these two numbers together.Calculation:
- Calculate product: Calculate the product of the decimal parts.Calculation:
- Add exponents: Add the exponents of .Since both numbers are multiplied by raised to the power of , we add the exponents according to the laws of exponents for multiplication.Calculation:
- Combine results: Combine the results of Step and Step to express the product in scientific notation.Since the product of the decimal parts is , which is not between and , we need to adjust it to fit the scientific notation format.Calculation: can be written as (since ).
- Adjust scientific notation: Adjust the scientific notation by combining the powers of .Now we combine the from the adjustment of the decimal part with the from the multiplication of the exponents.Calculation:
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
