AI tutor
Full solution
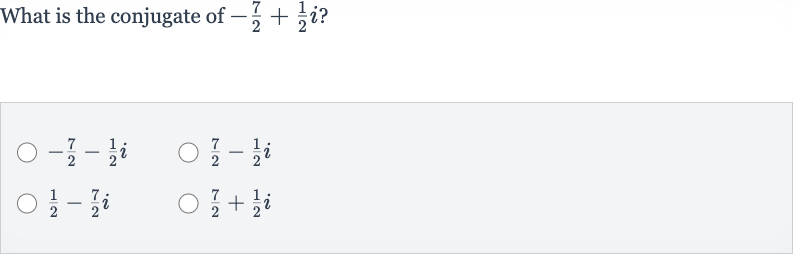
Q. What is the conjugate of ?
- Understand concept of conjugate: Understand the concept of a conjugate. The conjugate of a complex number is obtained by changing the sign of the imaginary part. The real part remains unchanged.
- Identify real and imaginary parts: Identify the real and imaginary parts of the given complex number.The given complex number is . Here, the real part is , and the imaginary part is .
- Change sign for conjugate: Change the sign of the imaginary part to find the conjugate.The conjugate of the given complex number is obtained by changing the sign of the imaginary part from positive to negative, while keeping the real part the same.So, the conjugate of is .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help