AI tutor
Full solution
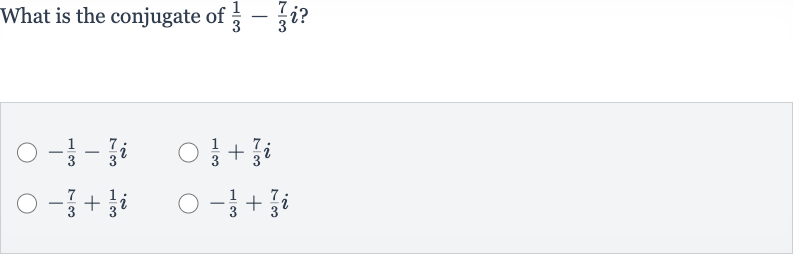
Q. What is the conjugate of ?
- Understand Conjugate Concept: Understand the concept of a conjugate. The conjugate of a complex number is , where and are real numbers. The conjugate is found by changing the sign of the imaginary part of the complex number.
- Identify Real and Imaginary Parts: Identify the real and imaginary parts of the given complex number.The given complex number is . Here, the real part is and the imaginary part is .
- Apply Conjugate Concept: Apply the concept of conjugate to the given complex number.To find the conjugate, we change the sign of the imaginary part while keeping the real part the same. Therefore, the conjugate of is .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help