Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the conjugate of
-(1)/(2)-(3)/(2)i ?

-(3)/(2)-(1)/(2)i

-(1)/(2)+(3)/(2)i

(1)/(2)+(3)/(2)i

(1)/(2)-(3)/(2)i

What is the conjugate of $-\frac{1}{2}-\frac{3}{2} i$ ? $\newline$ $-\frac{3}{2}-\frac{1}{2} i$ $\newline$ $-\frac{1}{2}+\frac{3}{2} i$ $\newline$ $\frac{1}{2}+\frac{3}{2} i$ $\newline$ $\frac{1}{2}-\frac{3}{2} i$

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

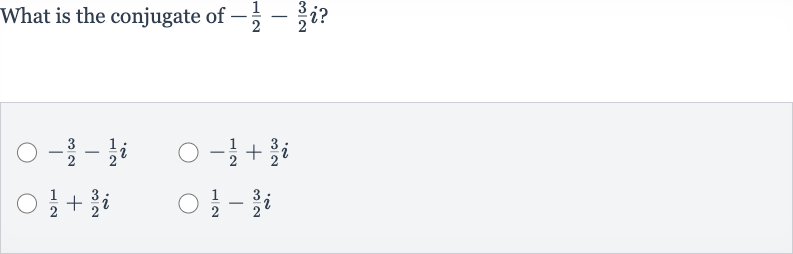
Q. What is the conjugate of

-\frac{1}{2}-\frac{3}{2} i

?

\newline

-\frac{3}{2}-\frac{1}{2} i

\newline

-\frac{1}{2}+\frac{3}{2} i

\newline

\frac{1}{2}+\frac{3}{2} i

\newline

\frac{1}{2}-\frac{3}{2} i

Identify Complex Number: The conjugate of a complex number is found by changing the sign of the imaginary part. The complex number in question is $-(\frac{1}{2})-(\frac{3}{2})i$ .
Find Conjugate: To find the conjugate, we keep the real part the same, which is $-(1)/(2)$ , and change the sign of the imaginary part from $-(3)/(2)i$ to $+(3)/(2)i$ .
Final Result: Therefore, the conjugate of $-(\frac{1}{2})-(\frac{3}{2})i$ is $-(\frac{1}{2})+(\frac{3}{2})i$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant