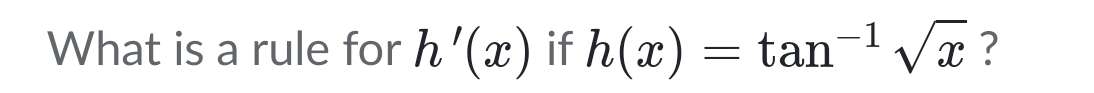Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is a rule for
h^(')(x) if
h(x)=tan^(-1)sqrtx ?

What is a rule for $h'(x)$ if $h(x)=\tan^{-1}\sqrt{x}$ ?

View step-by-step help

View step-by-step help

Domain and range of square root functions: equations

Full solution

Q. What is a rule for

h'(x)

if

h(x)=\tan^{-1}\sqrt{x}

?

Identify Functions: Identify the outer function and the inner function for the composition $h(x) = \arctan(\sqrt{x})$ . The outer function is $\arctan(u)$ and the inner function is $u = \sqrt{x}$ .
Apply Chain Rule: Apply the chain rule to differentiate $h(x) = \arctan(\sqrt{x})$ . The chain rule states that if a function $h$ can be written as a composition of two functions $f$ and $g$ , such that $h(x) = f(g(x))$ , then $h'(x) = f'(g(x)) \cdot g'(x)$ .
Differentiate Outer Function: Differentiate the outer function $f(u) = \arctan(u)$ with respect to $u$ . The derivative of $\arctan(u)$ with respect to $u$ is $f'(u) = \frac{1}{(1 + u^2)}$ .
Differentiate Inner Function: Differentiate the inner function $g(x) = \sqrt{x}$ with respect to $x$ . The derivative of $\sqrt{x}$ with respect to $x$ is $g'(x) = \frac{1}{2 \sqrt{x}}$ .
Substitute Derivatives: Substitute the derivatives of the outer and inner functions into the chain rule formula. $\newline$ $h'(x) = f'(g(x)) \cdot g'(x) = \frac{1}{1 + (\sqrt{x})^2} \cdot \frac{1}{2 \cdot \sqrt{x}}$ .
Simplify Expression: Simplify the expression for $h'(x)$ . $h'(x) = \frac{1}{2 \sqrt{x} (1 + x)}$ .

More problems from Domain and range of square root functions: equations

Question

What is the domain of this function?

\newline

y = \sqrt{x}

\newline

\newline

\{x|x \geq 0\}

\newline

\{x|x \leq 0\}

\newline

\{x | x < 0\}

\newline

\{x|x>0\}

Posted 9 months ago

Question

p

\newline

8 = \sqrt{p}

\newline

p =

Posted 9 months ago

Question

p

\newline

\sqrt{4p} = \sqrt{10 + 3p}

\newline

p =

Posted 5 months ago

Question

What is the domain of this function?

\newline

y = \sqrt{x}

Posted 5 months ago

Question

p

\newline

8 = \sqrt{p}

\newline

p =

Posted 9 months ago

Question

Find the derivative of

p(x)

\newline

p(x) = \ln(\sqrt{x})

\newline

p' (x) =

Posted 9 months ago

Question

Alice studies the relationship between climate and heart disease around the world.

\newline

H(t)

models the probability for the occurrence of heart disease (in percents relative to the global average) at an area where the temperature is

t

degrees Celsius.

\newline

According to Alice's model, when the temperature is

-5^{\circ}C

(which is the lowest temperature included in the model), the probability is

10\%

above average. Then the probability decreases until the temperature reaches

30^{\circ}C

(which is the highest temperature included in the model), where the probability is

20\%

\newline

Which number type is more appropriate for the domain of

H

\newline

1

\newline

\newline

(B) Real numbers

Posted 7 months ago

Question

The altitude at which we boil an egg affects how long it takes for the egg to achieve perfect hardness.

\newline

198

seconds to boil a perfect egg at the lowest place possible, the edge of the Dead Sea, which has an altitude of

-418

\newline

The highest place possible is the summit of Mount Everest which has an altitude of

8848

meters. It takes

209

seconds to boil a perfect egg there.

\newline

T(a)

models the time (in seconds) it takes to boil a perfect egg at an altitude of

a

\newline

Which number type is more appropriate for the domain of

T

\newline

1

\newline

\newline

(B) Real numbers

Posted 7 months ago

Question

f(x)=\sqrt{x-1}

\newline

f

is defined. What is the value of

f(10)

Posted 10 months ago

Question

h(x)=\sqrt{4 x}

\newline

h

is defined. What is the value of

h(9)

\newline

1

\newline

3

\newline

6

\newline

12

\newline

36

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant