Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

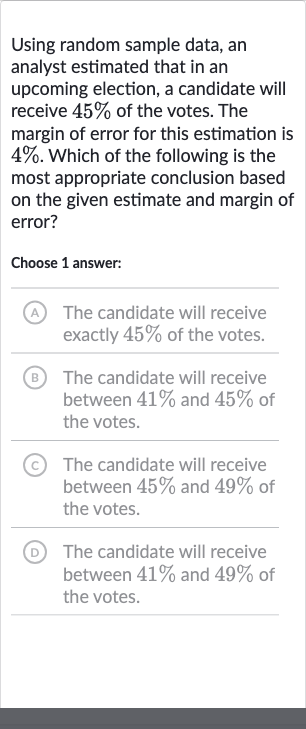
Using random sample data, an analyst estimated that in an upcoming election, a candidate will receive 45% of the votes. The margin of error for this estimation is 4%. Which of the following is the most appropriate conclusion based on the given estimate and margin of error? Choose 1 answer: (A) The candidate will receive exactly 45% of the votes. (B) The candidate will receive between 41% and 45% of the votes. (C) The candidate will receive between 45% and 49% of the votes. (D) The candidate will receive between 41% and 49% of the votes.

Using random sample data, an analyst estimated that in an upcoming election, a candidate will receive 45%45\% of the votes. The margin of error for this estimation is 4%4\%. Which of the following is the most appropriate conclusion based on the given estimate and margin of error?\newlineChoose 11 answer:\newline(A) The candidate will receive exactly 45%45\% of the votes.\newline(B) The candidate will receive between 41%41\% and 45%45\% of the votes.\newline(C) The candidate will receive between 45%45\% and 49%49\% of the votes.\newline(D) The candidate will receive between 41%41\% and 49%49\% of the votes.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Interpret confidence intervals for population meansright chevron icon

Full solution

Q. Using random sample data, an analyst estimated that in an upcoming election, a candidate will receive 45%45\% of the votes. The margin of error for this estimation is 4%4\%. Which of the following is the most appropriate conclusion based on the given estimate and margin of error?\newlineChoose 11 answer:\newline(A) The candidate will receive exactly 45%45\% of the votes.\newline(B) The candidate will receive between 41%41\% and 45%45\% of the votes.\newline(C) The candidate will receive between 45%45\% and 49%49\% of the votes.\newline(D) The candidate will receive between 41%41\% and 49%49\% of the votes.
  1. Margin of Error Explanation: Understand the concept of margin of error. The margin of error in a statistical estimate represents the range within which the true value is expected to lie with a certain level of confidence. In this case, the margin of error is 4%4\%, which means the true percentage of votes the candidate will receive could be 4%4\% higher or lower than the estimated 45%45\%.
  2. Calculate Lower Bound: Calculate the lower bound of the estimate.\newlineTo find the lower bound, subtract the margin of error from the estimated percentage.\newlineLower bound = Estimated percentage - Margin of error\newlineLower bound = 45%−4%45\% - 4\%\newlineLower bound = 41%41\%
  3. Calculate Upper Bound: Calculate the upper bound of the estimate.\newlineTo find the upper bound, add the margin of error to the estimated percentage.\newlineUpper bound =Estimated percentage+Margin of error= \text{Estimated percentage} + \text{Margin of error}\newlineUpper bound =45%+4%= 45\% + 4\%\newlineUpper bound =49%= 49\%
  4. Determine Range: Combine the lower and upper bounds to determine the range.\newlineThe candidate is estimated to receive between 41%41\% and 49%49\% of the votes, taking into account the margin of error.

More problems from Interpret confidence intervals for population means

Question
Michael surveyed 22 politicians from his state about their views on certain issues.\newlineIs this sample of citizens of the state likely to be biased?\newlineChoices:\newline[A]yes\newline[B]no
Get tutor helpright-arrow

Posted 7 months ago

Question
Read the following description of an experiment.\newlineA massage therapist has received complaints that the fragrance of her massage oil is unpleasant. She is testing whether a new oil will improve each clients' experience.\newlineThe massage therapist randomly sorts her clients into two groups. She massages 55 clients from the first group with the new oil and 55 from the other group with her usual oil. She asks all 1010 clients to rate their massages.\newlineIs this experiment statistically well designed?\newlineChoices:\newline[A]yes\newline[B]no
Get tutor helpright-arrow

Posted 7 months ago

Question
A random sample of 3535 four-door passenger vehicles had a mean gas mileage, in miles per gallon (mpg) (\mathrm{mpg}) , of 25.9mpg 25.9 \mathrm{mpg} . The estimate had a margin of error of 2.6mpg 2.6 \mathrm{mpg} at a 98% 98 \% confidence level. Of the following, which is the most plausible value for the true mean gas mileage of all four-door passenger vehicles?\newlineChoose 11 answer:\newline(A) 24mpg 24 \mathrm{mpg} \newline(B) 29mpg 29 \mathrm{mpg} \newline(C) 32mpg 32 \mathrm{mpg} \newline(D) 35mpg 35 \mathrm{mpg}
Get tutor helpright-arrow

Posted 8 months ago

Question
In a poll of 11,578578 randomly selected American adults, 44.8% 44.8 \% of the respondents said that airlines should allow in-flight calls on airplanes. The poll reported a margin of error of 2.5% 2.5 \% at a 95% 95 \% confidence level. Which of the following is most likely to be equal to the percentage of all American adults who would say that airlines should allow in-flight calls?\newlineChoose 11 answer:\newline(A) 40% 40 \% \newline(B) 43% 43 \% \newline(C) 48% 48 \% \newline(D) 95% 95 \%
Get tutor helpright-arrow

Posted 10 months ago

Question
Malik walked up and back down an empty 18 m 18 \mathrm{~m} long escalator at a constant rate. Since the escalator was going up at the time, it took him only 22.5 s 22.5 \mathrm{~s} . Going down took Malik 9090 s. Assume the escalator speed is constant.\newlineWhat was Malik's walking speed?\newlinems \frac{\mathrm{m}}{\mathrm{s}}
Get tutor helpright-arrow

Posted 8 months ago

Question
Two baseball players are warming up by throwing balls to the catcher. The two players are located 1010 yards apart, and the angle from each player to the catcher is 55∘55^{\circ} and 71∘71^{\circ}, respectively. What is the distance from the farthest baseball player to the catcher?\newlineA. 10.12510.125 yards\newlineB. 11.68711.687 yards\newlineC. 14.50114.501 yards\newlineD. 14.79014.790 yards
Get tutor helpright-arrow

Posted 8 months ago

Question
Select the outlier in the data set.\newline74,84,86,87,89,91,92,98,12674,84,86,87,89,91,92,98,126
Get tutor helpright-arrow

Posted 8 months ago

Question
Solve for p p .p8=79p=□\begin{array}{l}\frac{p}{8}=\frac{7}{9} \\p=\square\end{array}
Get tutor helpright-arrow

Posted 8 months ago

Question
Jelani needs to hire at least 1212 artists for an upcoming event. He needs to hire visual artists, who will be paid $300\$300 for the event, and performers, who will be paid $480\$480 for the event. His budget for paying the artists is no more than $6,000\$6,000. He must hire at least 44 visual artists and at least 33 performers. Which of the following does not satisfy all of the conditions described?\newlineChoose 11 answer:\newline(A) 44 visual artists and 1010 performers\newline(B) 88 visual artists and 88 performers\newline(C) $300\$30000 visual artists and 33 performers\newline(D) $300\$30022 visual artists and 44 performers
Get tutor helpright-arrow

Posted 8 months ago

Question
Factor.\newlinek2+9k+18k^2 + 9k + 18\newline____\newline
Get tutor helpright-arrow

Posted 8 months ago

View all (88)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant