AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
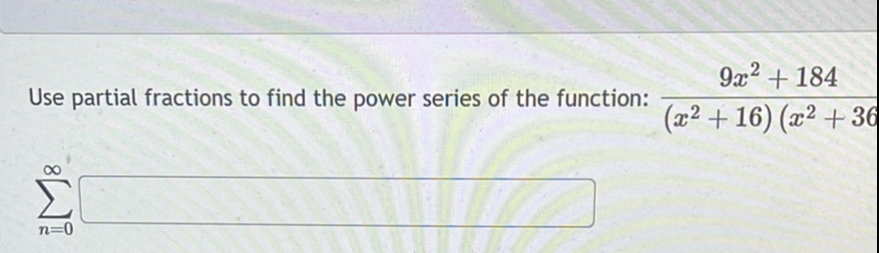
Use partial fractions to find the power series of the function: ____________
Full solution
Q. Use partial fractions to find the power series of the function: ____________
- Express Function: Step : Express the function using partial fractions.We need to decompose the function into simpler fractions.Assume .Multiply through by to clear the denominators:.
- Solve for A and B: Step : Solve for A and B.Equating coefficients, we get:For : For constant terms: Solving these equations: () ()From (), .Substitute into ():, .
- Write Decomposition: Step : Write the partial fraction decomposition.Substitute values of and back:.
- Expand Power Series: Step : Expand each term into a power series.For , use the geometric series formula:.For , similarly:.
