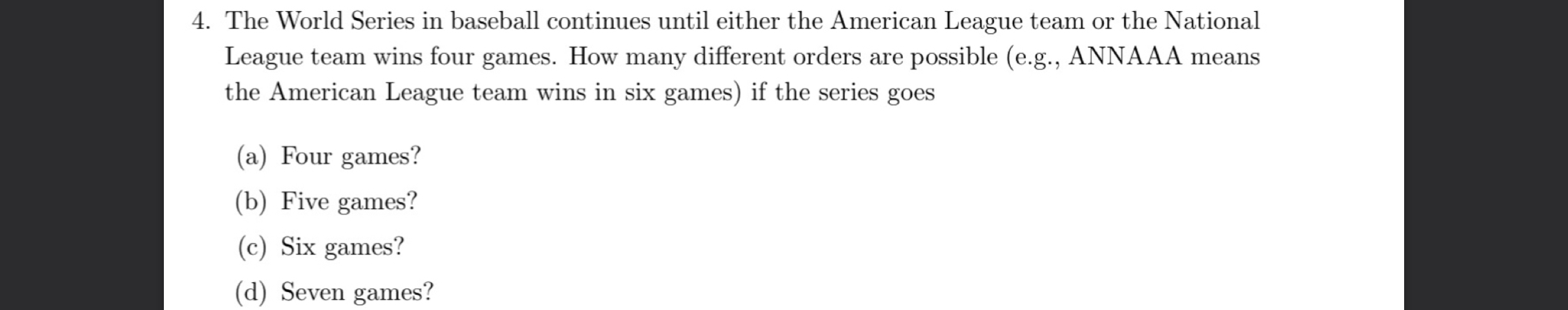
$4$ . The World Series in baseball continues until either the American League team or the National League team wins four games. How many different orders are possible (e.g., ANNAAA means the American League team wins in six games) if the series goes $\newline$ (a) Four games? $\newline$ (b) Five games? $\newline$ (c) Six games? $\newline$ (d) Seven games?

View step-by-step help

Home

Math Problems

Grade 8

Time and work rate problems

Full solution

4

. The World Series in baseball continues until either the American League team or the National League team wins four games. How many different orders are possible (e.g., ANNAAA means the American League team wins in six games) if the series goes

\newline

(a) Four games?

\newline

(b) Five games?

\newline

\newline

(d) Seven games?

Two Possible Orders: For a four-game series, one team must win all four games. There are only two possible orders: the American League team wins all four (AAAA) or the National League team wins all four (NNNN).
Calculate Different Orders: Calculate the number of different orders for a four-game series. Since there are only two possible outcomes, the number of different orders is $2^4$ .
Two Scenarios: For a five-game series, one team must win $4$ games and the other team wins $1$ . There are two scenarios: the American League team wins four ( $AAAA$ ) and the National League team wins one ( $N$ ), or vice versa. We need to find the number of ways to arrange four $A$ s and one $N$ .
Calculate Orders Using Combinations: Calculate the number of different orders for a five-game series using combinations. The formula for combinations is $C(n, k) = \frac{n!}{k!(n-k)!}$ , where $n$ is the total number of items and $k$ is the number of items to choose. Here, $n=5$ and $k=1$ for the one game the losing team wins. So, $C(5, 1) = \frac{5!}{1!(5-1)!} = 5$ .
Multiply by Two: Since there are two scenarios (American League wins or National League wins), we multiply the result by $2$ . So, $5 \times 2 = 10$ different orders for a five-game series.
Find Ways to Arrange: For a six-game series, one team must win $4$ games and the other team wins $2$ . We need to find the number of ways to arrange four $A$ s and two $N$ s, and vice versa.
Calculate Orders for Six-Game Series: Calculate the number of different orders for a six-game series using combinations. Here, $n=6$ and $k=2$ for the two games the losing team wins. So, $C(6, 2) = \frac{6!}{2!(6-2)!} = 15$ .
Multiply by Two: Since there are two scenarios (American League wins or National League wins), we multiply the result by $2$ . So, $15 \times 2 = 30$ different orders for a six-game series.
Find Ways to Arrange: For a seven-game series, one team must win four games and the other team wins three. We need to find the number of ways to arrange four $A$ s and three $N$ s, and vice versa.
Calculate Orders for Seven-Game Series: Calculate the number of different orders for a seven-game series using combinations. Here, $n=7$ and $k=3$ for the three games the losing team wins. So, $C(7, 3) = \frac{7!}{3!(7-3)!} = 35$ .
Multiply by Two: Since there are two scenarios (American League wins or National League wins), we multiply the result by $2$ . So, $35 \times 2 = 70$ different orders for a seven-game series.