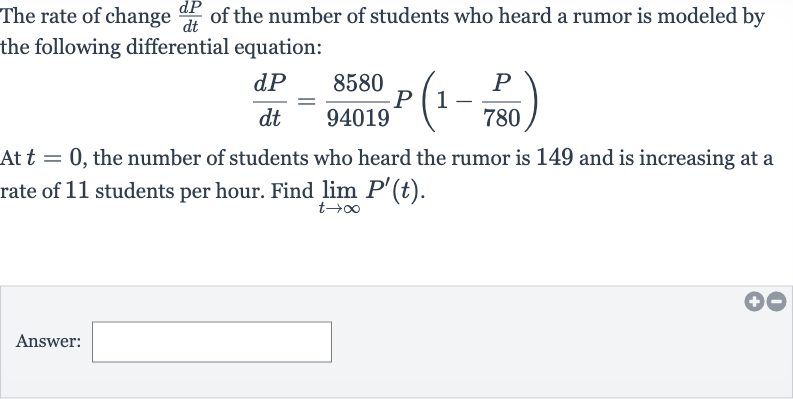
The rate of change (dP)/(dt) of the number of students who heard a rumor is modeled by the following differential equation: (dP)/(dt)=(8580)/(94019)P(1-(P)/( 780)) At t=0, the number of students who heard the rumor is 149 and is increasing at a rate of 11 students per hour. Find lim_(t rarr oo)P^(')(t). Answer:

Question

The rate of change  (dP)/(dt) of the number of students who heard a rumor is modeled by the following differential equation:  (dP)/(dt)=(8580)/(94019)P(1-(P)/( 780)) At  t=0, the number of students who heard the rumor is 149 and is increasing at a rate of 11 students per hour. Find  lim_(t rarr oo)P^(')(t). Answer:

Bytelearn · Accepted Answer

Given Differential Equation: We are given the differential equation: (dP)/(dt)=(8580)/(94019)P(1-(P)/(780)) We want to find the limit of P'(t) as t approaches infinity, which is essentially the long-term behavior of the rate of change of P.Analysis of Equation: To find the limit of P'(t) as t approaches infinity, we need to analyze the differential equation. The equation is a logistic growth model, which typically approaches a stable value as t approaches infinity.Stable Value and Carrying Capacity: In the logistic growth model, the stable value, also known as the carrying capacity, is the value of P where the growth rate P'(t) becomes zero. This happens when P equals the denominator of the fraction in the parenthesis, which is 780 in this case.Approaching Limit: So, as t approaches infinity, P will approach the carrying capacity, and the rate of change P'(t) will approach zero. This is because the term (1 - (P/780)) will approach zero as P approaches 780.Final Limit: Therefore, the limit of P'(t) as t approaches infinity is 0.

Full solution

More problems from Compound interest

Related topics