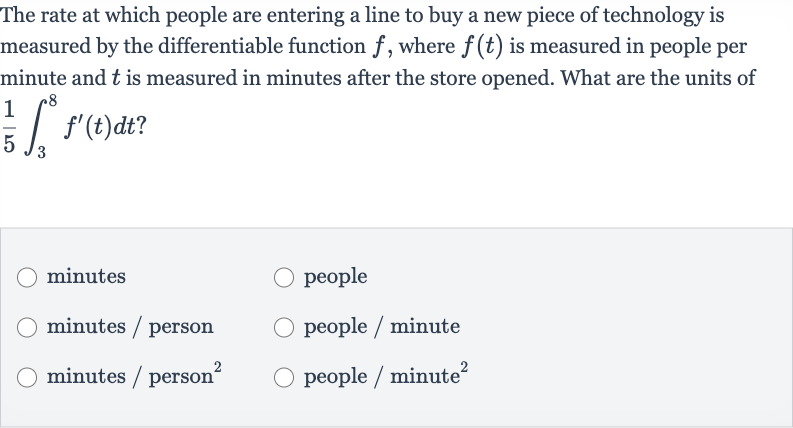
The rate at which people are entering a line to buy a new piece of technology is measured by the differentiable function f, where f(t) is measured in people per minute and t is measured in minutes after the store opened. What are the units of (1)/(5)int_(3)^(8)f^(')(t)dt? minutes people minutes / person people / minute minutes / person ^(2) people / minute ^(2)

Question

The rate at which people are entering a line to buy a new piece of technology is measured by the differentiable function  f, where  f(t) is measured in people per minute and  t is measured in minutes after the store opened. What are the units of  (1)/(5)int_(3)^(8)f^(')(t)dt? minutes people minutes / person people / minute minutes / person  ^(2) people / minute  ^(2)

Bytelearn · Accepted Answer

Given Integral Expression: The integral expression given is (1/5)∫_(3)^(8)f'(t)dt. We need to determine the units of this expression.Units of f'(t): First, let's understand the units of f(t) and f'(t). Since f(t) is measured in people per minute, f'(t) would be the rate of change of f(t), which gives us the units of people per minute squared (people/minute^2).Integral Interpretation: Now, let's look at the integral of f'(t) from 3 to 8. The integral of a rate of change gives us the net change over the interval. In this case, it would give us the net change in the number of people entering the line from t=3 minutes to t=8 minutes. The units of this integral would be the units of f(t), which is people per minute, multiplied by the units of t, which is minutes. Therefore, the units of the integral are people.Final Units: Finally, we multiply the integral by (1/5). Multiplying by a scalar does not change the units, so the units of the entire expression (1/5)∫_(3)^(8)f'(t)dt remain as people.

Full solution

More problems from Solve quadratic equations: word problems

Related topics