Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

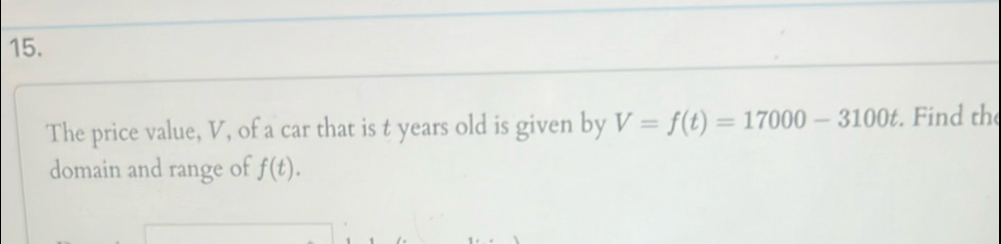
The price value,
V, of a car that is
t years old is given by
V=f(t)=17000-3100 t. Find thr domain and range of
f(t).

$\newline$ The price value, $V$ , of a car that is $t$ years old is given by $V=f(t)=17000-3100 t$ . Find thr domain and range of $f(t)$ .

View step-by-step help

View step-by-step help

Ratio and Quadratic equation

Full solution

Q.

\newline

The price value,

V

, of a car that is

t

years old is given by

V=f(t)=17000-3100 t

. Find thr domain and range of

f(t)

.

Identify Function Components: Identify the function and its components. $\newline$ $V = f(t) = 17000 - 3100t$
Determine Domain of $f(t)$ : Determine the domain of $f(t)$ . The domain of $f(t)$ is all values of $t$ for which the function makes sense. Since $t$ represents time in years, $t$ must be non-negative ( $t \geq 0$ ).
Calculate Zero Value Point: Calculate when the car value becomes zero or negative. $\newline$ Set $V = 0$ for boundary of domain. $\newline$ $0 = 17000 - 3100t$ $\newline$ $3100t = 17000$ $\newline$ $t = \frac{17000}{3100}$ $\newline$ $t = 5.48$
Interpret Domain Result: Interpret the result for domain. The car's value cannot be negative, so the maximum value for $t$ is when $V$ reaches zero, approximately at $t = 5.48$ years. Thus, the domain is $[0, 5.48]$ .
Determine Range of $f(t)$ : Determine the range of $f(t)$ . The range is the set of all possible values of $V$ . From $t = 0$ to $t = 5.48$ , $V$ decreases from $17000$ to $0$ .

More problems from Ratio and Quadratic equation

Question

Solve by completing the square.

\newline

m^2 - 10m - 29 = 0

\newline

Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.

\newline

`m` = ____ or `m` = _____

Posted 2 months ago

Question

g(x)

g(x)

is the translation

5

f(x)=x^2

\newline

Write your answer in the form

a(x–h)^2+k

a

h

k

\newline

g(x)=

Posted 2 months ago

Question

What is the range of this quadratic function?

\newline

y = x^2 - 4x + 4

\newline

\newline

\left\{y \mid y \geq 2\right\}

\newline

\left\{y \mid y \leq 0\right\}

\newline

\left\{y \mid y \geq 0\right\}

\newline

\text{all real numbers}

Posted 2 months ago

Question

Write the equation of the parabola that passes through the points

(1,0)

(2,0)

(3,\text{–}16)

. Write your answer in the form

y = a(x – p)(x – q)

a

p

q

are integers, decimals, or simplified fractions.

\newline

Posted 2 months ago

Question

Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.

\newline

f^2 + 8f + \_\_\_\_\_

Posted 2 months ago

Question

h

\newline

h^2 + 39h = 0

\newline

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

\newline

Posted 2 months ago

Question

Write a quadratic function with zeros

-9

-7

\newline

Write your answer using the variable

x

and in standard form with a leading coefficient of

1

\newline

f(x) = \_\_\_\_\_

Posted 2 months ago

Question

Find the equation of the axis of symmetry for the parabola

y = x^2

\newline

Simplify any numbers and write them as proper fractions, improper fractions, or integers.

\newline

\underline{\hspace{3cm}}

Posted 3 months ago

Question

g(x)

g(x)

is the translation

8

f(x) = x^2

\newline

Write your answer in the form

a(x – h)^2 + k

a

h

k

\newline

g(x) =

\newline

Posted 3 months ago

Question

x

\newline

x^2 = 1

\newline

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

\newline

Posted 3 months ago