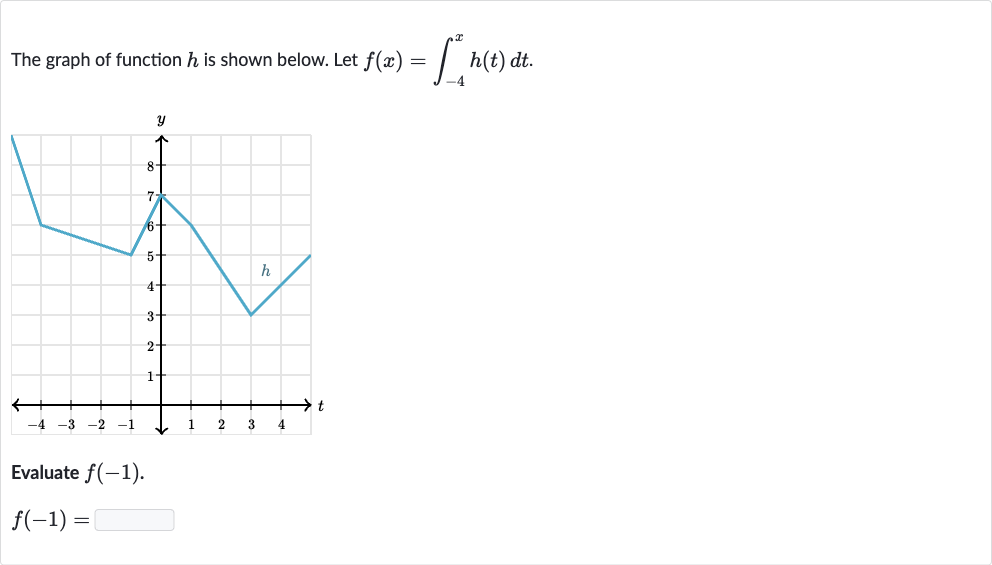Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The graph of function h is shown below. Let f(x)=int_(-4)^(x)h(t)dt. Evaluate f(-1). f(-1)=

The graph of function h h is shown below. Let f(x)=∫−4xh(t)dt f(x)=\int_{-4}^{x} h(t) d t .\newlineEvaluate f(−1) f(-1) .\newlinef(−1)= f(-1)=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Evaluate rational expressions IIright chevron icon

Full solution

Q. The graph of function h h is shown below. Let f(x)=∫−4xh(t)dt f(x)=\int_{-4}^{x} h(t) d t .\newlineEvaluate f(−1) f(-1) .\newlinef(−1)= f(-1)=
  1. Identify Area Range: Identify the area under the graph of h(t)h(t) from −4-4 to −1-1.
  2. Calculate Geometric Shapes: Calculate the area of each geometric shape under the graph from −4-4 to −1-1.
  3. Sum Areas for Total: Sum the areas to find the total area, which is the value of f(−1)f(-1).
  4. Find f(−1)f(-1) Value: f(−1)=(Area of shapes under the graph from−4to−1)f(-1) = (\text{Area of shapes under the graph from} -4 \text{to} -1).

More problems from Evaluate rational expressions II

Question
Divide. Write the quotient in lowest terms.\newline179÷45= 1 \frac{7}{9} \div \frac{4}{5}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline14÷118= \frac{1}{4} \div 1 \frac{1}{8}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline114÷125= 1 \frac{1}{4} \div 1 \frac{2}{5}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline58÷113= \frac{5}{8} \div 1 \frac{1}{3}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline445÷112= 4 \frac{4}{5} \div 1 \frac{1}{2}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline212÷223= 2 \frac{1}{2} \div 2 \frac{2}{3}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline338÷9= 3 \frac{3}{8} \div 9=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline3310÷147= 3 \frac{3}{10} \div 1 \frac{4}{7}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline423÷7= 4 \frac{2}{3} \div 7=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline318÷123= 3 \frac{1}{8} \div 1 \frac{2}{3}=
Get tutor helpright-arrow

Posted 3 months ago

View all (16)