Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The graph of function h is shown below. Let f(x)=int_(3)^(x)h(t)dt. Evaluate f(4). f(4)=

The graph of function h h is shown below. Let f(x)=∫3xh(t)dt f(x)=\int_{3}^{x} h(t) d t .\newlineEvaluate f(4) f(4) .\newlinef(4)= f(4)=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Evaluate rational expressions IIright chevron icon

Full solution

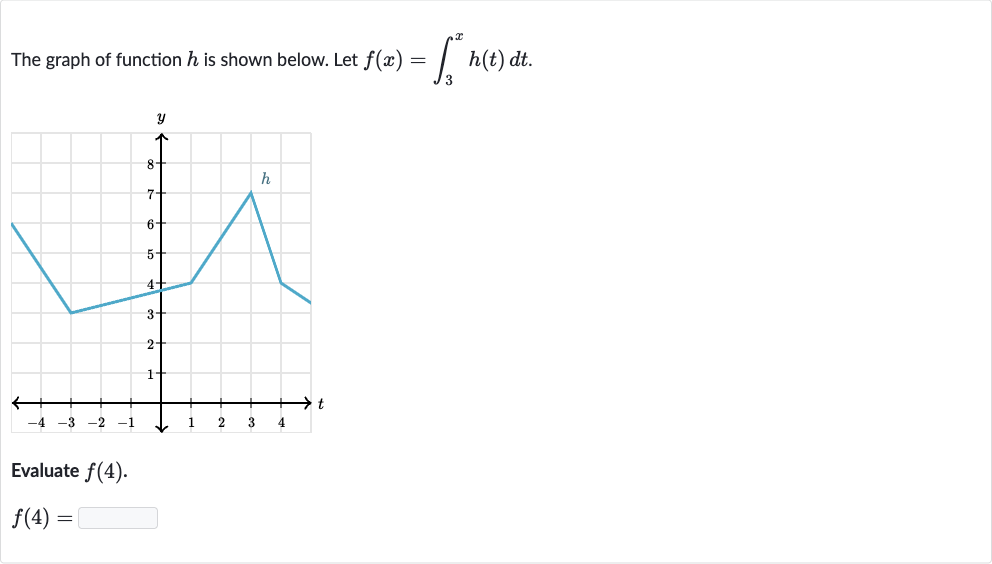
Q. The graph of function h h is shown below. Let f(x)=∫3xh(t)dt f(x)=\int_{3}^{x} h(t) d t .\newlineEvaluate f(4) f(4) .\newlinef(4)= f(4)=
  1. Substitute xx with 44: Substitute xx with 44 in the function f(x)f(x).f(4)=∫34h(t) dtf(4) = \int_{3}^{4} h(t) \, dt
  2. Determine area under curve: Look at the graph of h(t)h(t) to determine the area under the curve from 33 to 44. Assuming the graph shows a rectangle or a trapezoid from 33 to 44, calculate the area.

More problems from Evaluate rational expressions II

Question
Divide. Write the quotient in lowest terms.\newline179÷45= 1 \frac{7}{9} \div \frac{4}{5}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline14÷118= \frac{1}{4} \div 1 \frac{1}{8}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline114÷125= 1 \frac{1}{4} \div 1 \frac{2}{5}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline58÷113= \frac{5}{8} \div 1 \frac{1}{3}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline445÷112= 4 \frac{4}{5} \div 1 \frac{1}{2}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline212÷223= 2 \frac{1}{2} \div 2 \frac{2}{3}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline338÷9= 3 \frac{3}{8} \div 9=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline3310÷147= 3 \frac{3}{10} \div 1 \frac{4}{7}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline423÷7= 4 \frac{2}{3} \div 7=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline318÷123= 3 \frac{1}{8} \div 1 \frac{2}{3}=
Get tutor helpright-arrow

Posted 3 months ago

View all (16)