Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The graph of function f is shown below. Let h(x)=int_(-4)^(x)f(t)dt. Evaluate h(-2). h(-2)=

The graph of function f f is shown below. Let h(x)=∫−4xf(t)dt h(x)=\int_{-4}^{x} f(t) d t .\newlineEvaluate h(−2) h(-2) .\newlineh(−2)= h(-2)=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Evaluate rational expressions IIright chevron icon

Full solution

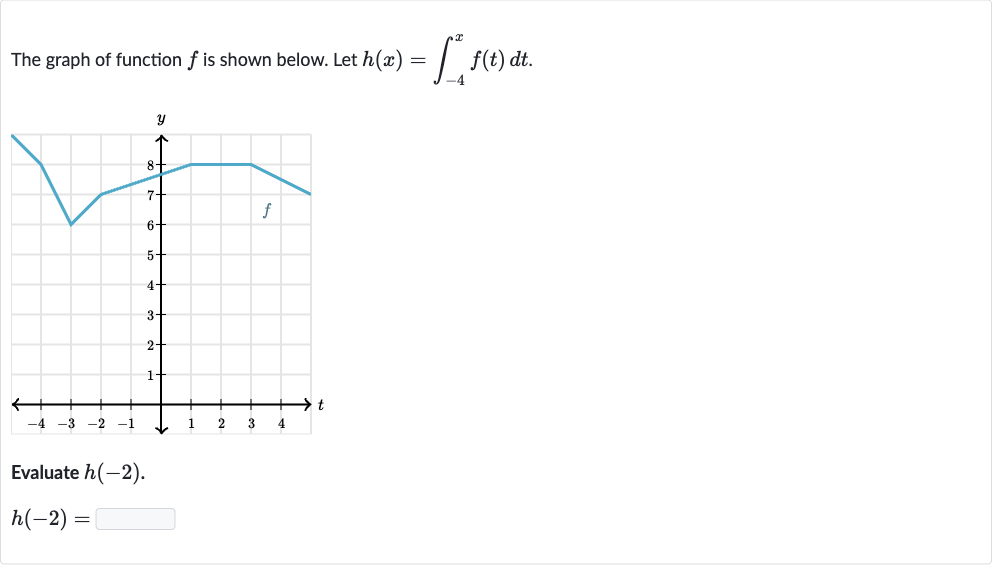
Q. The graph of function f f is shown below. Let h(x)=∫−4xf(t)dt h(x)=\int_{-4}^{x} f(t) d t .\newlineEvaluate h(−2) h(-2) .\newlineh(−2)= h(-2)=
  1. Understand h(x)h(x): Understand the definition of h(x)h(x).h(x)h(x) is the definite integral of f(t)f(t) from −4-4 to xx.
  2. Find area from −4-4 to −2-2: Find the area under the graph of f(t)f(t) from −4-4 to −2-2. This area represents h(−2)h(-2).
  3. Calculate total area: Calculate the area under the graph.\newlineAssuming the graph is provided and the area can be calculated directly.

More problems from Evaluate rational expressions II

Question
Divide. Write the quotient in lowest terms.\newline179÷45= 1 \frac{7}{9} \div \frac{4}{5}=
Get tutor helpright-arrow

Posted 4 months ago

Question
Divide. Write the quotient in lowest terms.\newline14÷118= \frac{1}{4} \div 1 \frac{1}{8}=
Get tutor helpright-arrow

Posted 4 months ago

Question
Divide. Write the quotient in lowest terms.\newline114÷125= 1 \frac{1}{4} \div 1 \frac{2}{5}=
Get tutor helpright-arrow

Posted 4 months ago

Question
Divide. Write the quotient in lowest terms.\newline58÷113= \frac{5}{8} \div 1 \frac{1}{3}=
Get tutor helpright-arrow

Posted 4 months ago

Question
Divide. Write the quotient in lowest terms.\newline445÷112= 4 \frac{4}{5} \div 1 \frac{1}{2}=
Get tutor helpright-arrow

Posted 4 months ago

Question
Divide. Write the quotient in lowest terms.\newline212÷223= 2 \frac{1}{2} \div 2 \frac{2}{3}=
Get tutor helpright-arrow

Posted 4 months ago

Question
Divide. Write the quotient in lowest terms.\newline338÷9= 3 \frac{3}{8} \div 9=
Get tutor helpright-arrow

Posted 4 months ago

Question
Divide. Write the quotient in lowest terms.\newline3310÷147= 3 \frac{3}{10} \div 1 \frac{4}{7}=
Get tutor helpright-arrow

Posted 4 months ago

Question
Divide. Write the quotient in lowest terms.\newline423÷7= 4 \frac{2}{3} \div 7=
Get tutor helpright-arrow

Posted 4 months ago

Question
Divide. Write the quotient in lowest terms.\newline318÷123= 3 \frac{1}{8} \div 1 \frac{2}{3}=
Get tutor helpright-arrow

Posted 4 months ago

View all (16)