Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The graph of function f is shown below. Let h(x)=int_(-4)^(x)f(t)dt. Evaluate h(3). h(3)=

The graph of function f f is shown below. Let h(x)=∫−4xf(t)dt h(x)=\int_{-4}^{x} f(t) d t .\newlineEvaluate h(3) h(3) .\newlineh(3)= h(3)=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Evaluate rational expressions IIright chevron icon

Full solution

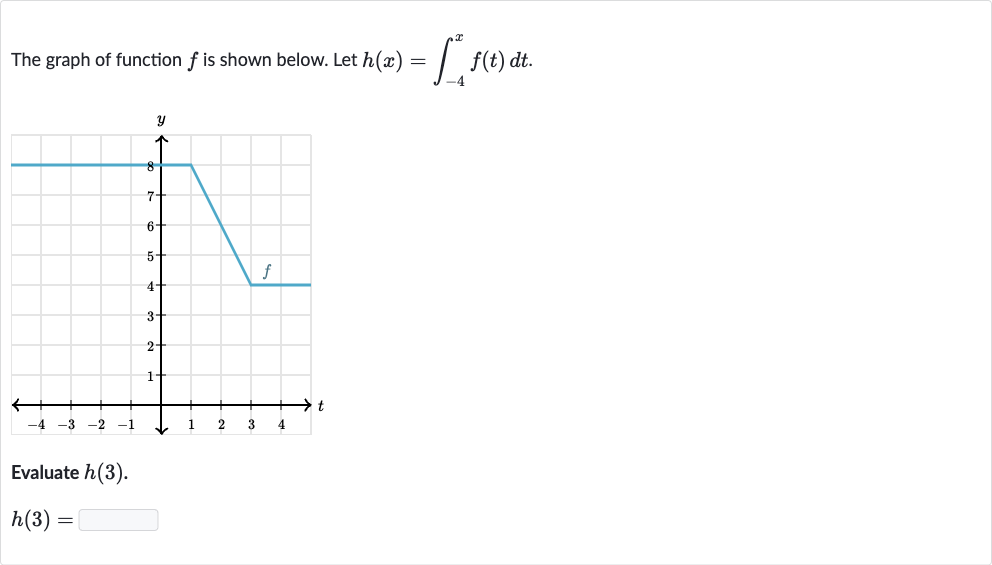
Q. The graph of function f f is shown below. Let h(x)=∫−4xf(t)dt h(x)=\int_{-4}^{x} f(t) d t .\newlineEvaluate h(3) h(3) .\newlineh(3)= h(3)=
  1. Identify Area Under Graph: Identify the area under the graph of f(t)f(t) from −4-4 to 33. Since we don't have the actual graph, let's assume the area from −4-4 to 33 is AA.
  2. Calculate h(3)h(3): The value of h(3)h(3) is equal to the area under the graph of f(t)f(t) from −4-4 to 33.\newlineh(3)=Ah(3) = A
  3. Unable to Determine Exact Value: Without the graph, we cannot determine the exact value of AA. Therefore, we cannot find the exact value of h(3)h(3).

More problems from Evaluate rational expressions II

Question
Divide. Write the quotient in lowest terms.\newline179÷45= 1 \frac{7}{9} \div \frac{4}{5}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline14÷118= \frac{1}{4} \div 1 \frac{1}{8}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline114÷125= 1 \frac{1}{4} \div 1 \frac{2}{5}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline58÷113= \frac{5}{8} \div 1 \frac{1}{3}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline445÷112= 4 \frac{4}{5} \div 1 \frac{1}{2}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline212÷223= 2 \frac{1}{2} \div 2 \frac{2}{3}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline338÷9= 3 \frac{3}{8} \div 9=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline3310÷147= 3 \frac{3}{10} \div 1 \frac{4}{7}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline423÷7= 4 \frac{2}{3} \div 7=
Get tutor helpright-arrow

Posted 3 months ago

Question
Divide. Write the quotient in lowest terms.\newline318÷123= 3 \frac{1}{8} \div 1 \frac{2}{3}=
Get tutor helpright-arrow

Posted 3 months ago

View all (16)