Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

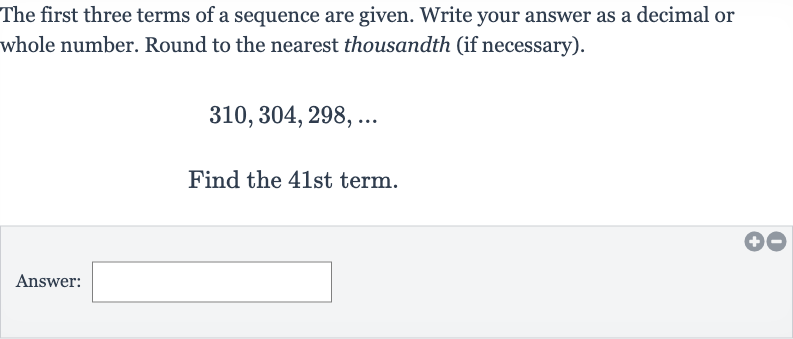
The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary). 310,304,298,dots Find the 41st term. Answer:

The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary).\newline310,304,298,… 310,304,298, \ldots \newlineFind the 4141st term.\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Partial sums of geometric seriesright chevron icon

Full solution

Q. The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary).\newline310,304,298,… 310,304,298, \ldots \newlineFind the 4141st term.\newlineAnswer:
  1. Determine common difference: First, we need to determine the common difference of the sequence by subtracting any term from the previous term.\newlineCommon difference = 304−310304 - 310
  2. Calculate common difference: Now, let's calculate the common difference.\newlineCommon difference = 304−310=−6304 - 310 = -6
  3. Use nth term formula: Next, we use the formula for the nth term of an arithmetic sequence, which is:\newlinenth term = first term + (n−1)×common difference(n - 1) \times \text{common difference}\newlineWe want to find the 41st41^{\text{st}} term, so n=41n = 41.
  4. Substitute values: Let's substitute the values into the formula to find the 41st41^{\text{st}} term.41st41^{\text{st}} term = 310+(41−1)×(−6)310 + (41 - 1) \times (-6)
  5. Calculate inside parentheses: Now, we calculate the term inside the parentheses and then multiply by the common difference.\newline41st41^{\text{st}} term = 310+(40)×(−6)310 + (40) \times (-6)
  6. Perform multiplication: Next, we perform the multiplication. 41st41^{\text{st}} term = 310+(−240)310 + (-240)
  7. Add numbers: Finally, we add the numbers to find the 41st41^{st} term.\newline41st41^{st} term =310−240=70= 310 - 240 = 70

More problems from Partial sums of geometric series

Question
Find the sum of the finite arithmetic series. ∑n=110(7n+4)\sum_{n=1}^{10} (7n+4)\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`
Get tutor helpright-arrow

Posted 5 months ago

Question
Type the missing number in this sequence: `2, 4 8`, ______,`32`
Get tutor helpright-arrow

Posted 5 months ago

Question
What kind of sequence is this? 2,10,50,250,…2, 10, 50, 250, \ldots Choices:Choices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 5 months ago

Question
What is the missing number in this pattern? 1,4,9,16,25,36,49,64,81,____1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_
Get tutor helpright-arrow

Posted 7 months ago

Question
Classify the series. ∑n=012(n+2)3 \sum_{n = 0}^{12} (n + 2)^3 \newlineChoices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the first three partial sums of the series.\newline1+6+11+16+21+26+⋯1 + 6 + 11 + 16 + 21 + 26 + \cdots\newlineWrite your answers as integers or fractions in simplest form.\newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the third partial sum of the series. \newline3+9+15+21+27+33+⋯3 + 9 + 15 + 21 + 27 + 33 + \cdots\newlineWrite your answer as an integer or a fraction in simplest form. \newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the first three partial sums of the series. \newline1+7+13+19+25+31+⋯1 + 7 + 13 + 19 + 25 + 31 + \cdots\newlineWrite your answers as integers or fractions in simplest form. \newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 9 months ago

Question
Does the infinite geometric series converge or diverge?\newline1+34+916+2764+⋯1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots\newlineChoices:\newline[A]converge\text{[A]converge}\newline[B]diverge\text{[B]diverge}
Get tutor helpright-arrow

Posted 5 months ago

View all (96)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant