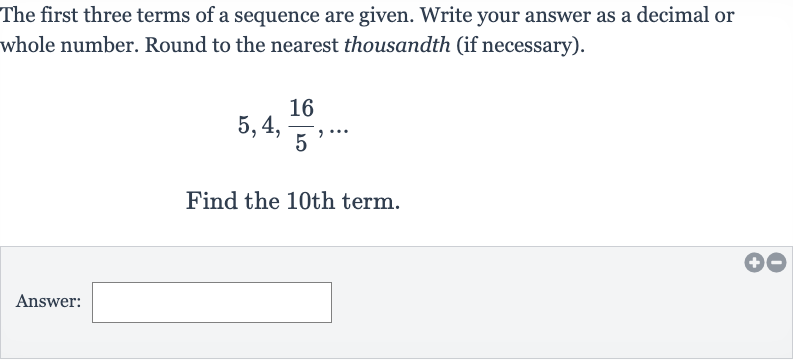
The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary). 5,4,(16)/(5),dots Find the 10th term. Answer:

Question

The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary).  5,4,(16)/(5),dots Find the 10th term. Answer:

Bytelearn · Accepted Answer

Determine Pattern: To find the 10th term of the sequence, we first need to determine the pattern or rule that the sequence follows. We can start by looking at the differences between consecutive terms.Identify Differences: The difference between the first term (5) and the second term (4) is -1. The difference between the second term (4) and the third term (16/5) is (16/5) - 4 = (16/5) - (20/5) = -4/5. This suggests that the sequence might be an arithmetic sequence with a common difference of -1/5.Confirm Arithmetic Sequence: To confirm that the sequence is arithmetic with a common difference of -1/5, we can check the difference between the third term (16/5) and what would be the fourth term if we subtract another -1/5 from the third term. The fourth term would be (16/5) - (1/5) = (15/5) = 3. This confirms our pattern, as the difference is indeed -1/5.Apply Formula: Now that we have established that the sequence is arithmetic with a common difference of -1/5, we can use the formula for the nth term of an arithmetic sequence: a_n = a_1 + (n - 1)d, where a_n is the nth term, a_1 is the first term, n is the term number, and d is the common difference.Calculate 10th Term: We are looking for the 10th term (a_10). We know that a_1 = 5 and d = -1/5. Plugging these values into the formula, we get a_10 = 5 + (10 - 1)(-1/5).Round to Nearest Thousandth: Calculating the 10th term, we have a_10 = 5 + 9(-1/5) = 5 - 9/5 = 5 - 1.8 = 3.2.Since the problem asks us to round to the nearest thousandth if necessary, and our answer is already to the nearest tenth, no further rounding is required. The 10th term of the sequence is 3.2.

The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary). $\newline$ $5,4, \frac{16}{5}, \ldots$ $\newline$ Find the $10$ th term. $\newline$ Answer:

Full solution

More problems from Find trigonometric functions using a calculator

Related topics

The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary).\newline5,4,165,… 5,4, \frac{16}{5}, \ldots 5,4,516​,…\newlineFind the 101010th term.\newlineAnswer:

The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary). $\newline$ $5,4, \frac{16}{5}, \ldots$ $\newline$ Find the $10$ th term. $\newline$ Answer: