The expression $(y^{2}-t^{2})(y+k)$ can be written as $y^{3}+36 y^{2}-9 y+s$ where $t, k$ , and $s$ are constants. What is the value of $s$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $-324$ $\newline$ (B) $-54$ $\newline$ (C) $54$ $\newline$ (D) $324$

View step-by-step help

Home

Math Problems

Algebra 1

Transformations of quadratic functions

Full solution

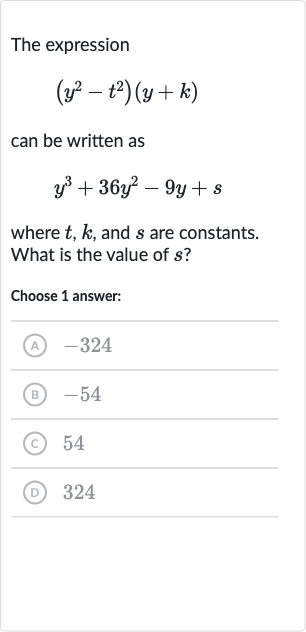
Q. The expression

(y^{2}-t^{2})(y+k)

can be written as

y^{3}+36 y^{2}-9 y+s

where

t, k

, and

s

are constants. What is the value of

s

\newline

Choose

1

answer:

\newline

(A)

-324

\newline

(B)

-54

\newline

(C)

54

\newline

(D)

324

Factorize Difference of Squares: We need to expand the expression $y^2 - t^2)(y + k)\ and compare it to \$y^3 + 36y^2 - 9y + s$ to find the value of $s$ .
Expand and Compare Expressions: First, recognize that $y^2 - t^2$ is a difference of squares and can be factored into $(y + t)(y - t)$ .
Identify Coefficients: Now, distribute $(y + t)(y - t)$ across $(y + k)$ to get the expanded form. $\newline$ $(y + t)(y - t)(y + k) = y(y^2 - t^2) + k(y^2 - t^2)$
Eliminate Terms: Expand $y(y^2 - t^2)$ to get $y^3 - yt^2$ .
Find Constant Term: Expand $k(y^2 - t^2)$ to get $ky^2 - kt^2$ .
Find Constant Term: Expand $k(y^2 - t^2)$ to get $ky^2 - kt^2$ .Combine the terms to get the full expanded expression: $y^3 - yt^2 + ky^2 - kt^2$ .
Find Constant Term: Expand $k(y^2 - t^2)$ to get $ky^2 - kt^2$ .Combine the terms to get the full expanded expression: $y^3 - yt^2 + ky^2 - kt^2$ .Now, compare the expanded expression to $y^3 + 36y^2 - 9y + s$ . We see that the coefficient of $y^2$ in the expanded expression is $k - t$ , which must equal $36$ from the given expression.
Find Constant Term: Expand $k(y^2 - t^2)$ to get $ky^2 - kt^2$ .Combine the terms to get the full expanded expression: $y^3 - yt^2 + ky^2 - kt^2$ .Now, compare the expanded expression to $y^3 + 36y^2 - 9y + s$ . We see that the coefficient of $y^2$ in the expanded expression is $k - t$ , which must equal $36$ from the given expression.The term $-yt^2$ has no corresponding term in $y^3 + 36y^2 - 9y + s$ , which means that $t$ must be $ky^2 - kt^2$ $0$ to eliminate the term $ky^2 - kt^2$ $1$ .
Find Constant Term: Expand $k(y^2 - t^2)$ to get $ky^2 - kt^2$ .Combine the terms to get the full expanded expression: $y^3 - yt^2 + ky^2 - kt^2$ .Now, compare the expanded expression to $y^3 + 36y^2 - 9y + s$ . We see that the coefficient of $y^2$ in the expanded expression is $k - t$ , which must equal $36$ from the given expression.The term $-yt^2$ has no corresponding term in $y^3 + 36y^2 - 9y + s$ , which means that $t$ must be $ky^2 - kt^2$ $0$ to eliminate the term $ky^2 - kt^2$ $1$ .With $t$ being $ky^2 - kt^2$ $0$ , the term $ky^2 - kt^2$ $4$ also disappears, leaving us with $ky^2 - kt^2$ $5$ as the only terms with $y^2$ and $ky^2 - kt^2$ $7$ .
Find Constant Term: Expand $k(y^2 - t^2)$ to get $ky^2 - kt^2$ . Combine the terms to get the full expanded expression: $y^3 - yt^2 + ky^2 - kt^2$ . Now, compare the expanded expression to $y^3 + 36y^2 - 9y + s$ . We see that the coefficient of $y^2$ in the expanded expression is $k - t$ , which must equal $36$ from the given expression. The term $-yt^2$ has no corresponding term in $y^3 + 36y^2 - 9y + s$ , which means that $t$ must be $ky^2 - kt^2$ $0$ to eliminate the term $ky^2 - kt^2$ $1$ . With $t$ being $ky^2 - kt^2$ $0$ , the term $ky^2 - kt^2$ $4$ also disappears, leaving us with $ky^2 - kt^2$ $5$ as the only terms with $y^2$ and $ky^2 - kt^2$ $7$ . Since there is no $ky^2 - kt^2$ $7$ term in $y^3 + 36y^2 - 9y + s$ , $y^3 - yt^2 + ky^2 - kt^2$ $0$ must also be $ky^2 - kt^2$ $0$ to eliminate the term $y^3 - yt^2 + ky^2 - kt^2$ $2$ .
Find Constant Term: Expand $k(y^2 - t^2)$ to get $ky^2 - kt^2$ .Combine the terms to get the full expanded expression: $y^3 - yt^2 + ky^2 - kt^2$ .Now, compare the expanded expression to $y^3 + 36y^2 - 9y + s$ . We see that the coefficient of $y^2$ in the expanded expression is $k - t$ , which must equal $36$ from the given expression.The term $-yt^2$ has no corresponding term in $y^3 + 36y^2 - 9y + s$ , which means that $t$ must be $ky^2 - kt^2$ $0$ to eliminate the term $ky^2 - kt^2$ $1$ .With $t$ being $ky^2 - kt^2$ $0$ , the term $ky^2 - kt^2$ $4$ also disappears, leaving us with $ky^2 - kt^2$ $5$ as the only terms with $y^2$ and $ky^2 - kt^2$ $7$ .Since there is no $ky^2 - kt^2$ $7$ term in $y^3 + 36y^2 - 9y + s$ , $y^3 - yt^2 + ky^2 - kt^2$ $0$ must also be $ky^2 - kt^2$ $0$ to eliminate the term $y^3 - yt^2 + ky^2 - kt^2$ $2$ .Now we know that $y^3 - yt^2 + ky^2 - kt^2$ $3$ and $y^3 - yt^2 + ky^2 - kt^2$ $4$ , so the term $y^3 - yt^2 + ky^2 - kt^2$ $5$ in the expression $y^3 + 36y^2 - 9y + s$ is the constant term left over, which is $ky^2 - kt^2$ $4$ .
Find Constant Term: Expand $k(y^2 - t^2)$ to get $ky^2 - kt^2$ .Combine the terms to get the full expanded expression: $y^3 - yt^2 + ky^2 - kt^2$ .Now, compare the expanded expression to $y^3 + 36y^2 - 9y + s$ . We see that the coefficient of $y^2$ in the expanded expression is $k - t$ , which must equal $36$ from the given expression.The term $-yt^2$ has no corresponding term in $y^3 + 36y^2 - 9y + s$ , which means that $t$ must be $ky^2 - kt^2$ $0$ to eliminate the term $ky^2 - kt^2$ $1$ .With $t$ being $ky^2 - kt^2$ $0$ , the term $ky^2 - kt^2$ $4$ also disappears, leaving us with $ky^2 - kt^2$ $5$ as the only terms with $y^2$ and $ky^2 - kt^2$ $7$ .Since there is no $ky^2 - kt^2$ $7$ term in $y^3 + 36y^2 - 9y + s$ , $y^3 - yt^2 + ky^2 - kt^2$ $0$ must also be $ky^2 - kt^2$ $0$ to eliminate the term $y^3 - yt^2 + ky^2 - kt^2$ $2$ .Now we know that $y^3 - yt^2 + ky^2 - kt^2$ $3$ and $y^3 - yt^2 + ky^2 - kt^2$ $4$ , so the term $y^3 - yt^2 + ky^2 - kt^2$ $5$ in the expression $y^3 + 36y^2 - 9y + s$ is the constant term left over, which is $ky^2 - kt^2$ $4$ .Substitute $y^3 - yt^2 + ky^2 - kt^2$ $3$ and $y^3 - yt^2 + ky^2 - kt^2$ $4$ into $ky^2 - kt^2$ $4$ to find $y^3 - yt^2 + ky^2 - kt^2$ $5$ . $y^3 + 36y^2 - 9y + s$ $2$ $y^3 + 36y^2 - 9y + s$ $3$
Find Constant Term: Expand $k(y^2 - t^2)$ to get $ky^2 - kt^2$ .Combine the terms to get the full expanded expression: $y^3 - yt^2 + ky^2 - kt^2$ .Now, compare the expanded expression to $y^3 + 36y^2 - 9y + s$ . We see that the coefficient of $y^2$ in the expanded expression is $k - t$ , which must equal $36$ from the given expression.The term $-yt^2$ has no corresponding term in $y^3 + 36y^2 - 9y + s$ , which means that $t$ must be $ky^2 - kt^2$ $0$ to eliminate the term $ky^2 - kt^2$ $1$ .With $t$ being $ky^2 - kt^2$ $0$ , the term $ky^2 - kt^2$ $4$ also disappears, leaving us with $ky^2 - kt^2$ $5$ as the only terms with $y^2$ and $ky^2 - kt^2$ $7$ .Since there is no $ky^2 - kt^2$ $7$ term in $y^3 + 36y^2 - 9y + s$ , $y^3 - yt^2 + ky^2 - kt^2$ $0$ must also be $ky^2 - kt^2$ $0$ to eliminate the term $y^3 - yt^2 + ky^2 - kt^2$ $2$ .Now we know that $y^3 - yt^2 + ky^2 - kt^2$ $3$ and $y^3 - yt^2 + ky^2 - kt^2$ $4$ , so the term $y^3 - yt^2 + ky^2 - kt^2$ $5$ in the expression $y^3 + 36y^2 - 9y + s$ is the constant term left over, which is $ky^2 - kt^2$ $4$ .Substitute $y^3 - yt^2 + ky^2 - kt^2$ $3$ and $y^3 - yt^2 + ky^2 - kt^2$ $4$ into $ky^2 - kt^2$ $4$ to find $y^3 - yt^2 + ky^2 - kt^2$ $5$ . $y^3 + 36y^2 - 9y + s$ $2$ $y^3 + 36y^2 - 9y + s$ $3$ However, we made a mistake. We should have compared the constant terms directly instead of assuming $t$ and $y^3 - yt^2 + ky^2 - kt^2$ $0$ are zero. Let's correct this by comparing the constant term $ky^2 - kt^2$ $4$ from the expanded expression to the constant term $y^3 - yt^2 + ky^2 - kt^2$ $5$ in the given expression $y^3 + 36y^2 - 9y + s$ .