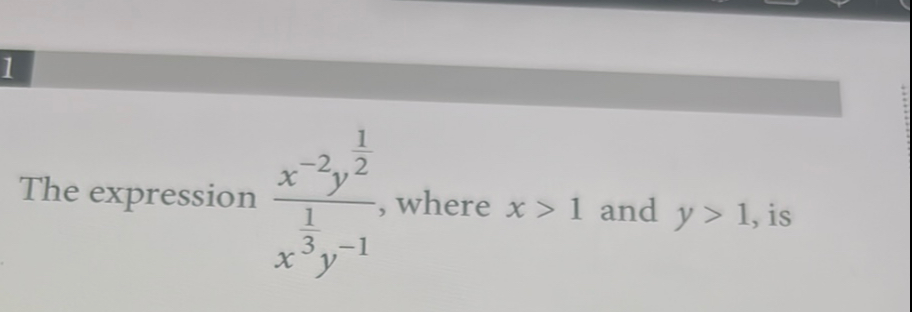AI tutor
Full solution
Q. The expression , where and , is
- Combine terms: We have the expression . To simplify, we will use the properties of exponents to combine the terms and the terms separately.
- Simplify terms: First, we simplify the terms using the property of exponents that states when dividing like bases, we subtract the exponents: . So, for the terms, we have .
- Simplify terms: To subtract the exponents, we need a common denominator. The common denominator for (which is ) and is . So we convert to to get the same denominator as . Now we have .
- Combine y terms: Next, we simplify the y terms using the same property of exponents: .
- Combine and terms: Adding the exponents for terms, we get .
- Final expression: Now we combine the simplified and terms to get the final simplified expression: .
- Problem completion: Since the question prompt asks for the expression to be simplified and we have done so, we have completed the problem.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help